lestat128 a dit:
Vous ne retirez pas 12 fois 0.75,
En y repensant après coup c'est effectivement ce que je m'apprêtais à vérifier
lestat128 a dit:
mais vous retirez 12 fois 0.75 à ce qui reste de l'année précédente.
Donc à la fin de la première année il vous reste 99.25, à la fin de la 2ieme année, il vous reste 98.505625 et non 98.50, et ainsi de suite jusqu'à la 12ieme année d'où les 91.36211251.
Chaque année l'on retire
une fois 075% de ce qui reste l'année précédente
lestat128 a dit:
En l’occurrence la valeur nominale n'est plus 100 mais les 91.36211251 qui restent.
Non tel que vous l'expliquez la valeur de calcul diminue progressivement de 0,75% chaque année pour atteindre 91,321 seulement la douzième année.
pchmartin a dit:
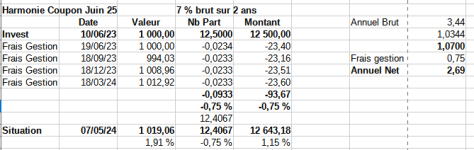
Si ça peut alimenter ce débat, voilà le réél sur Harmonie Coupon Juin 2025 investit sur Ex Direct l'an dernier .
Les frais sont de 0,75% de la valeur de Juin 23 après 4 prélèvements trimestriels... on pourra voir mi juin comment est traitée la 2ème année .
Afficher la pièce jointe 28657
Merci, ce document est en effet très éclairant.
Mais je ne sais si ce produit est identique à celui objet des échanges antérieurs pour les raisons suivantes:
1) - Contrairement à ce qui est dit ci-dessus le calcul du prélèvement des 0,75% de parts pour compenser les frais de gestion est toujours pratiqué sur la base initiale de 12,50 parts; il n'y a pas de dégressivité à l'intérieur de la même année. A voir pour les années suivantes ?
=> 12,50 x 0,75% / 4 = 0,0234275
Mais le fait que ce résultat soit tantôt arrondi à 0,0234 ou 0,0233 laisse supposer que, trimestre par trimestre, le calcul est prorata temporis ?
2) - Le montant réel de ces frais en euros ne dépend pas que du nombre de parts; il dépend aussi de la valeur du portefeuille :
FG première année (19/06) : 1.000€ x 0,0234 = 23,40€
FG deuxième année (18/09)
: 994,03€ x 0,0234 = 23,16€
3) - Ils sont prélevés tous les trimestres et non pas annuellement; un calcul actuariel de rentabilité se traduirait donc une régression du taux réel par rapport au même calcul avec des prélèvements annuels
Pour le produit objet des échanges initiaux si l'on suppose donc :
1) - Que le le nombre de parts est réduit chaque année de 0,75% par rapport au solde antérieur (= dégressivité en nombre de parts prélevées en paiement des frais de gestion)
2) - Que ces prélèvement sont annuels
3) - Que
la valeur de la part reste inchangée; égale à sa valeur initiale (?)
=> Le calcul du taux de rentabilité suit la logique de l'équation indiquée page 174 ci-dessus mais en en modifiant les termes pour tenir compte tant de la dégressivité des parts prélevées en paiement des frais de gestion que d'un seul paiement in fine du solde du portefeuille plus des intérêts.
=> Soit un taux der rendement (=TRI) de 3,41% (NB - page 174 je trouvais 3,42%)
A noter encore que, suivant ces hypothèses et ce calcul les intérêts perçu nets de FG seraient de 58,16€ alors que la fiche produit indique 51,60€
???
A toutes fins utiles.
Cdt