Produits structurés

[Phil17000]

Faux et cela en dévient gênant.
Je me répète, l'investisseur ne peut pas décider de sortir et encaisser les coupons passés, seuls la SG en tant qu'émetteur à le droit de décider de la fin du produit et dans ce cas elle paye les coupons.
Si l'investisseur décide de sortir, il le fait avec la valorisation de la part telle qu'elle est sur le marché secondaire et cela n'a rien à voir avec les coupons (ou partiellement mais ce n'est pas aussi simple).

Est-ce que quelqu'un peut intervenir et expliquer à cette personne comment marche ce type de produit parce que moi j'abandonne.
Phil ? vous êtes motivés ?

Je pense qu'on a à peu près fait le tour du sujet. Je rajoute juste que l'option offerte à l'émetteur de pouvoir racheter l'obligation quand il le souhaite a une valeur d'autant plus élevée que la durée est longue (en l'occurrence 12 ans) et c'est grâce à cette caractéristique que le taux affiché peut sembler à première vue attractif.

 

[Aristide]

Bonjour,

Faux et cela en dévient gênant.
Je me répète, l'investisseur ne peut pas décider de sortir et encaisser les coupons passés, seuls la SG en tant qu'émetteur à le droit de décider de la fin du produit et dans ce cas elle paye les coupons.

Mais nulle part je n'ai écrit cela; j'ai seulement détaillé les calculs.
En revanche c'est vous même qui avez cité une sortie possible avant la fin :

Votre message laisse penser à ceux qui le lise que s'ils sortent avant la fin ils auront des coupons (même pourvus d'intérêts) hors ce n'est pas le cas et potentiellement source de mauvaise surprise.

Si l'investisseur décide de sortir, il le fait avec la valorisation de la part telle qu'elle est sur le marché secondaire et cela n'a rien à voir avec les coupons (ou partiellement mais ce n'est pas aussi simple).

Dans lesdits tableaux la valeur "Rembt" intègre bien les coupons bruts échus; détaillant ces calculs.
Je ne pouvais dire le contraire puisque c'est ainsi; désolé !

Donc pour être clair et conclure :
+ La SG décide "la fin du produit"; les tableaux et les calculs qu'ils présentent sont corrects.
+ Mais si c'est l'investisseur qui "décide de sortir" ces tableaux et leurs calculs ne servent à rien.

 

[rémois]

Le tableau fourni par pchmartin que j'ai décortiqué dans Excel montre bien que le coupon brut de 5,05% est ajouté chaque année au montant initial.

C'est ce que j'ai nommé "une sorte de capitalisation" en précisant bien d'ailleurs qu'il ne s'agissait pas d'une vraie capitalisation puisque cet ajout des intérêts bruts n'était pas lui même productif d'intérêts.

Et, chaque année l'on voit que c'est cette somme "capital + intérêts bruts" qui, multiplié par le nombre de parts résiduel, donne la valeur de remboursement au terme de ladite année.

Aristide, vous vous trompez et vous vous obstinez.

La brochure officielle de ce produit est très claire et c'est LA seule référence (bien sûr).
Les coupons ne sont versés qu'à la fin du produit, in fine et d'un seul bloc... soit à l'échéance finale, au bout des 12 ans (60,6% bruts)... soit quand l'émetteur décide de fermer le produit avant les 12 ans (fort probable). C'est aussi simple que cela.

"Les tableaux" que vous citez comme référence et comme preuves ne sont que des calculs qu'un forumeur a fait pour lui sur son tableur, simplement pour vérifier le TRA exact qui faisait débat dans ce topic. Ça ne voulait en rien dire que les coupons sont versés chaque année.

Tant que le produit continue, le souscripteur ne touche aucun coupon. Et s'il décide de sortir de lui-même... idem, aucun coupon.


(c'était pour répondre à la supplique de lestat128 qui demandait du soutien)

 

[Aristide]

Si on s'intéresse aux remboursements anticipés, on trouve dans la brochure:
l’Emetteur pourra rembourser par anticipation les Titres, à la Date de Remboursement Optionnel(i) (i de 1 à 11) selon les dispositions suivantes relatives à chaque Titre :
Montant de Remboursement Optionnel(i) = Valeur Nominale × [100% + (i × 5.05%)]
et comme vous l'indiquez le nombre de parts diminue au fil de l'eau .. soit de -0,75% par an comme constaté sur Harmonie Coupon Juin25 ; soit de -0,85% comme les UCs de Ex Direct ( je vérifierai aux prochains frais de gestion en Juin)). Le tableau est alors le suivant:
Afficher la pièce jointe 28687
on retrouve bien les 60,6% sur la valeur : Taux d’Intérêt : 60,6% payable à terme échu
Si le nombre de parts diminue de -0,75% , le rendement capitalisé varie de 4,26% si remboursé en 2025 et 3,25% si remboursé en 2036 ! ( pour -0,85% ca varie entre 4,16% et 3,14%).

Compte tenu de ma situation ( +70 ans, objectif transmission) .. c'est un bon plan ! même si je suis remboursé
dans 3 ans ..

Désolé si, concernant le tableau joint par pchmartin c'est bien ainsi que vous le dites; je lui laisse le soin de confirmer ou non.

Mais le texte publié avec ce tableau indique bien :

"Si on s'intéresse aux remboursements anticipés, on trouve dans la brochure:
"l’Emetteur pourra rembourser par anticipation les Titres, à la Date de Remboursement Optionnel(i) (i de 1 à 11) selon les dispositions suivantes relatives à chaque Titre :
Montant de Remboursement Optionnel(i) = Valeur Nominale × [100% + (i × 5.05%)]"

Donc si l’Émetteur rembourse les titres par anticipation, comme indiqué ci-dessus, les coupons bruts échus sont bien pris en compte de la valeur de remboursement
=> C'est le texte de la brochure officielle dont vous faites état.

Et vous le confirmez d'ailleurs dans votre intervention ci-dessus :

Les coupons ne sont versés qu'à la fin du produit, in fine et d'un seul bloc... soit à l'échéance finale, au bout des 12 ans (60,6% bruts)... soit quand l'émetteur décide de fermer le produit avant les 12 ans (fort probable)

Je répète donc que mon tableau ne fait que détailler les calculs dudit tableau dans cette hypothèse.

Je vous remercie donc de ne pas me faire dire ce que je n'ai ni dit ni écrit.

Et je répète aussi :

Donc pour être clair et conclure :
+ La SG décide "la fin du produit"; les tableaux et les calculs qu'ils présentent sont corrects.
+ Mais si c'est l'investisseur qui "décide de sortir" ces tableaux et leurs calculs ne servent à rien.

Cdt

 

[Phil17000]

A présent que nous sommes globalement d'accord sur le fonctionnement du produit, la question qu'on peut avoir tendance à se poser en tant qu'investisseur est :

Quelle est la probabilité de remboursement du produit aux différentes dates de rappel ?

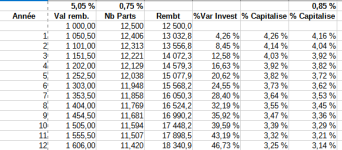
Ci-dessous le tableau de @pchmartin

Parce que toucher 4.26% sur un an ou 3.25% sur douze ans ce n'est pas du tout la même histoire.

Sur ce forum, nous avons la chance d'avoir des personnes à l'aise avec les statistiques et les mathématiques et je serais très intéressé par leur avis sur ce sujet.

Mon approche très rustique serait de partir du coût résiduel annualisé pour SG aux différentes dates de rappel et de le comparer avec le coût pour SG d'une obligation de même durée résiduelle.

Voici la courbe de taux pour SG :


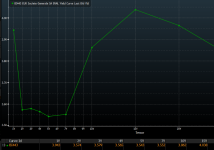
Je pars du principe que la courbe des taux intègre le chemin le plus probable des taux, en dehors de la maturité 1 an qui est biaisée par les taux monétaires.

J'obtiens le tableau suivant :


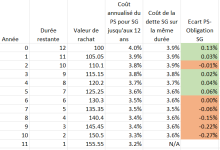
J'en déduis que :
1/ La probabilité la plus élevée est un rachat dès la première année.
2/ Si le produit n'a pas été rappelé au cours des 5 premières années, alors il est peu probable qu'il le soit avant l'échéance des 12 ans.

Je rappelle que c'est une approche minimaliste, à prendre avec des pincettes, et qu'il doit être possible de faire quelque chose de plus correct d'un point de vue mathématique et statistique (un arbre binomial, une simulation de Monte-Carlo, ou autre ?).
Preneur de vos avis.

 

[lestat128]

Bonjour,
Assez d'accord avec vous, mais il y a un élément que nous ne maitrisons pas, c'est l'aspect marketing.
Cette analyse semble très probable pour le Impulsion 3 qui est un cousin germain, mais pour ce coupon qui est uniquement accueilli au sein d'une assurance vie commercialisée par Boursobank, la société générale voudra peut-être faire plaisir à ces clients et ne pas appliquer le call.
Le volonté de la SG de développer boursobank même au détriment de ses agences est quand même assez forte.
C'est un avis vraiment personnel bien sur.

 

[lestat128]

(c'était pour répondre à la supplique de lestat128 qui demandait du soutien)

Merci mais malheureusement assez inutile vu ce qui a suivi

 

[Aristide]

Ce qui a suivi ce n'est que la confirmation de la réalité.

"Si on s'intéresse aux remboursements anticipés, on trouve dans la brochure:
"l’Emetteur pourra rembourser par anticipation les Titres, à la Date de Remboursement Optionnel(i) (i de 1 à 11) selon les dispositions suivantes relatives à chaque Titre :
Montant de Remboursement Optionnel(i) = Valeur Nominale × [100% + (i × 5.05%)]"

Et je répète aussi une troisième fois :

Donc pour être clair et conclure :
+ La SG décide "la fin du produit"; les tableaux et les calculs qu'ils présentent sont corrects.
+ Mais si c'est l'investisseur qui "décide de sortir" ces tableaux et leurs calculs ne servent à rien.

 

[Aristide]

J'en déduis que :
1/ La probabilité la plus élevée est un rachat dès la première année.
2/ Si le produit n'a pas été rappelé au cours des 5 premières années, alors il est peu probable qu'il le soit avant l'échéance des 12 ans.

Je rappelle que c'est une approche minimaliste, à prendre avec des pincettes, et qu'il doit être possible de faire quelque chose de plus correct d'un point de vue mathématique et statistique (un arbre binomial, une simulation de Monte-Carlo, ou autre ?).
Preneur de vos avis.

Ce sujet c'est de la la très haute finance qui, dans les Établissements concernés, mobilise, à côté du directeur financier et du Trésorier Principal, les services d'économistes, prévisionnistes et actuaires qui "planchent" au mieux des intérêts de leurs employeurs, sur la notion de "Taux Forward"

Comment calculer les taux forward à partir des taux zéro-coupon ? Définition & exemple
[lien réservé abonné]

Exemple Taux forward 6 ans dans 9 ans
Tx-Fd mensuel = [[(1+ x,xx%)^(6+9)) / (1+ (y,yy%)^9)]^ (1/6)] – 1 »

Xx taux 15 ans
Yy taux 9 ans

A toutes fins utiles pour votre information.

Pour ce qui me concerne je ne m'y risque pas et, compte tenu de la mauvaise foi et l'état d'esprit malveillant d'un participant je sors de ce post.

 

[pchmartin]

Bonjour,
Assez d'accord avec vous, mais il y a un élément que nous ne maitrisons pas, c'est l'aspect marketing.
Cette analyse semble très probable pour le Impulsion 3 qui est un cousin germain, mais pour ce coupon qui est uniquement accueilli au sein d'une assurance vie commercialisée par Boursobank, la société générale voudra peut-être faire plaisir à ces clients et ne pas appliquer le call.
Le volonté de la SG de développer boursobank même au détriment de ses agences est quand même assez forte.
C'est un avis vraiment personnel bien sur.

Ce type de produit Harmonie Coupon ( ou Sérénité Coupon) existe depuis Janvier 23 avec un horizon de 2 ans et un taux 2 ans entre 6,2% et 7,5% .. l'enveloppe maximale étant entre 50M€ et 75M€. Il y en a eu 1 par mois pendant 13 mois. [lien réservé abonné] ..
Et brutalement, ils sortent un produit 12 ans avec Coupon de 60,6% ( donc beaucoup plus fort) ; remboursement anticipé par émetteur possible avec enveloppe maximale de 60M€ !! Mais on ne peut pas dire que c'est beaucoup mis en avant sur le site où il faut cliquer sur 1 offre de produits à capital garantis à échéance [lien réservé abonné] ..
La question est donc: pourquoi ?? peut être pour fidéliser les vieux clients existants avec du Eurossima / Netissima et éviter qu'ils partent à la concurrence avec les offres Euro + Bonus .. ou ????

 

[Phil17000]

Ce sujet c'est de la la très haute finance qui, dans les Établissements concernés, mobilise, à côté du directeur financier et du Trésorier Principal, les services d'économistes, prévisionnistes et actuaires qui "planchent" au mieux des intérêts de leurs employeurs, sur la notion de "Taux Forward"

Merci pour la piste.
Intuitivement je sens bien que le taux forward doit intervenir quelque part (notamment entre l'année 7 et l'année 12 où la courbe est pentue), mais ce n'est pas ma spécialité et c'est un peu flou.
Preneur d'idées s'il y a des experts sur le sujet.

 

[briblu86]

Dans cet interview l'intervenante reconnaît que c'est très bien margé pour tous les intermédiaires. On le savait mais elle a le mérite de le reconnaître
[lien réservé abonné]

 

[dede02]

Salut tout le monde, simple curiosité sur les produit structurés. Vous en pensez quoi de Exigence 23 ?

[lien réservé abonné]

 

[niklos]

Vous en pensez quoi de Exigence 23 ?

Encore une indice de référence décrémenté de 5% ce qui rend le produit... Euh... Pas intéressant de mon point de vue.

 

[dede02]

J'ai toujours une méfiance envers ce genre de produits. ça parait toujours trop beau

 

[jodel140]

J'ai toujours une méfiance envers ce genre de produits. ça parait toujours trop beau

Tant qu'à faire dans le commentaire laconique ...

soit les 37ème et 38ème remboursements positifs (pour moi et mon épouse)
Bonne journée

 

[dede02]

J'ai toujours une méfiance envers ce genre de produits. ça parait toujours trop beau

Tant qu'à faire dans le commentaire laconique ...
Afficher la pièce jointe 29522
soit les 37ème et 38ème remboursements positifs (pour moi et mon épouse)
Bonne journée

Ce n'est peut être pas la même offre. C'est comme partout il doit y avoir les bons et les mauvais produits.

 

[régalade]

7,85% par an c'est pas mal ^^

 

[jodel140]

Dans cet interview l'intervenante reconnaît que c'est très bien margé pour tous les intermédiaires. On le savait mais elle a le mérite de le reconnaître
[lien réservé abonné]

Interview qui résume assez bien la situation pour tous les intervenants. Et tant ça 'marge' correctement pour le client (moi ) je suis ravi que ça marge pour les intermédiaires.
Les questions que je me pose sont toujours ;
- est-ce que je comprend ce que l'on me propose
- est-ce que j'accepte la rémunération pour le risque
Les questions que je ne me pose pas;
- Est-ce que l'intermédiaire se sucre
- Est-ce que je pourrais faire mieux avec un autre produit
Ces produits représentent environ 20% de mes AV pour 11 dossiers en cours. Je réinvesti quand il sont remboursés, pour l'instant (depuis 14 ans) toujours. Je n'ai perdu que sur un seul dossier que j'ai revendu par anticipation.
Ce commentaire n'est que mon expérience personnelle. Pas un conseil d'investissement.
Pour les conseils avisés il faut reprendre les posts de @niklos et @Axiles, par exemple

 

[régalade]

Autant je comprends qu'on ne se demande pas ce que gagne l'intermédiaire tant que ça nous rapporte, à nous, autant je ne comprends pas qu'on ne regarde pas s'il existe mieux ailleurs.