AiePépito
Contributeur régulier
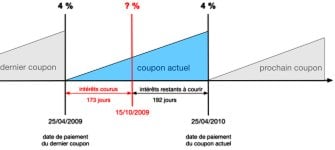
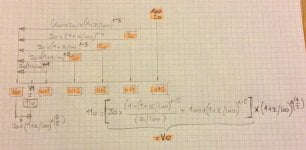
dans cette formule vous avez bien actualisé le coupon et le remboursement alors pourquoi dans la grosse formule vous ne le faites pas?Aristide a dit:110 = (c1 x(1+x)^(-1/2)) + (c2 x(1+x)^(-1,5)) + (c3 x(1+x)^(-2,5) + (c4 x(1+x)^(-3,5) + ((100+c5) x(1+x)^(-4,5)
84,77€ = (0,375€ x (1+Tpt)^(-1)) + (0,375€ x (1+Tpt)^(-2)) +………..+(0,375€ x (1+Tpt)^(-24)) + (0,375€ x (1+Tpt)^(-25)) + (100€ x (1+Tpt)^(-((25)+(2/3)))) [
ici dans votre formule il n’y a que le dernier coupon et le remboursement qui sont totalement actualisés.
pour les autres coupons ils sont actualisés aussi mais pas complètement


 !!
!!