Marioux
Contributeur régulier
Lundi 24 janvier 2022 :
Bonjour à tous !
Toujours aucune réaction ?
Ni contestation, ni approbation ?
La terreur règne vraiment dans ce forum ! ...
Ou bien, trop compliqué jusqu’ici ? Pourquoi pas ?
Il faudrait simplifier, condenser, se mettre à la portée du Lecteur éventuel !
Revenons à des tableaux d’amortissement moins longs, plus faciles à analyser : 3 échéances devraient suffire ;
Et puis, tant qu’on y est, un taux annuel de l’intérêt conventionnel, stipulé et fixé par écrit, constant (Ça ira ?)
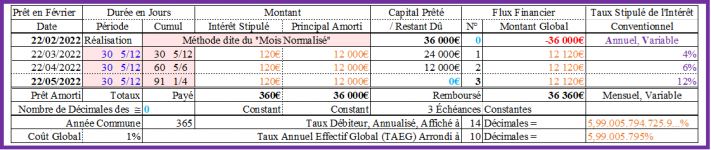
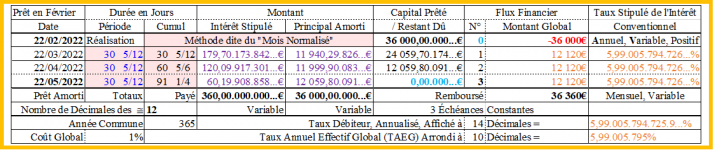
Reprenons donc le prêt, rappelé le vendredi 07/01/2022, d’un capital de 36 000€, emprunté le 22/02/2022, assorti d’un intérêt global stipulé de 211,20€, toujours remboursé mensuellement, les 22/03/2022, 22/04/2022 et 22/05/2022, mai cette fois, par échéances de montant constant (36 211,20€ / 3M = 12 070,40€), avec un taux annuel de l’intérêt conventionnel, déterminé pour cela, à 3,5166%, par calcul itératif ou par la fonction "Valeur cible" d’EXCEL par exemple, et dont le tableau d’amortissement est le suivant :
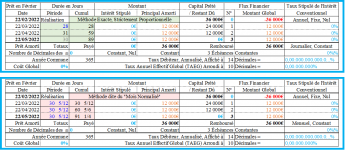
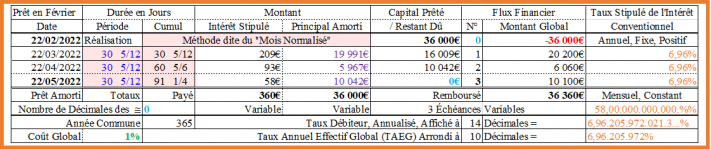
Méthode dite du "Mois Normalisé" (Le remboursement est pseudopériodique ! ...) :
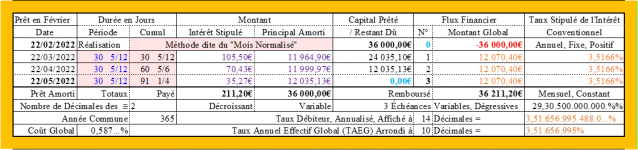
Échéance 1 :
Intérêt : 3,5166%/An / 12Mois/An x 36 000€ = 105,49 8€ ≈ 105,50€ ;
Principal amorti : 12 070,40€ - 105,50€ = 11 964,90€ ; CRD : 36 000€ - 11 964,90€ = 24 035,10€.
Échéance 2 :
Intérêt : 3,5166%/An / 12Mois/An x 24 035,10€ = 70,43 486 055€ ≈ 70,43€ ;
Principal amorti : 12 070,40€ - 70,43€ = 11 999,97€ ; CRD : 24 035,10€ - 11 999,97€ = 12 035,13€.
Échéance 3 :
Intérêt : 3,5166%/An / 12Mois/An x 12 035,13€ = 35,26 894 846 5€ ≈ 35,27€ ;
Principal amorti : 12 035,13€ ; CRD : 12 035,13€ - 12 035,13€ = 0€, au terme du prêt !
Taux débiteur annualisé = TAEG : 3,51 656 995…% ≈ 3,5166% (Taux annuel de l’intérêt conventionnel) : OK !
Évidemment, ces calculs et cette démonstration ne venant pas de lui, Aristide qui pense être le seul à détenir la vérité, pourra toujours contester virulemment ce qui est écrit ci-dessus, au prétexte que des calculs doivent être exacts et que, du coup, d’après lui, il ne faut surtout pas arrondir les montants mensuels des intérêts !
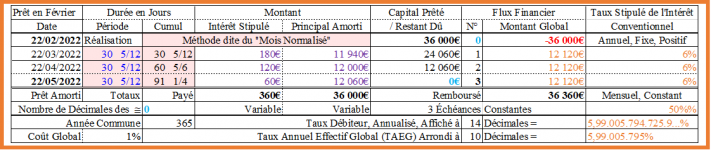
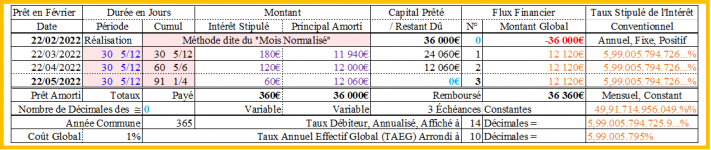
Même s’il se gardera d’afficher tous les chiffres significatifs au-delà des centimes, pour lui, le véritable tableau d’amortissement devrait, sans doute, être celui-ci ! :
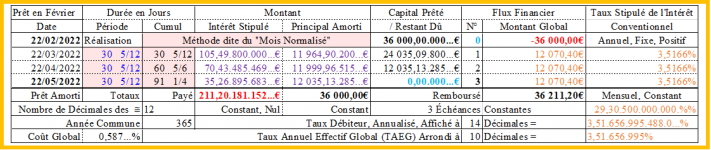
Là, c’est sûr, avec cette théorie "fumeuse" et un flux financier strictement identique, d'où un même coût du prêt, égal, ici, au montant global de l'intérêt stipulé, et strictement les mêmes TAEG et taux débiteur, nous voilà bien avancés !
Et quand on sait que par la méthode Exacte ci-après, le montant des intérêts de la première échéance, sans arrondi au centime, s’élève à 97,11 596 712 328 7…€ ≠< 105,498€ ;
La différence étant de 105,49 8€ - 97,11 596 712 328 7…€ = 8,38 203 287 671 2…€ ≈ 8,38…€ ;
On se demande bien à quoi rimerait de ne pas arrondir les montants respectifs à un "pauvre" centime (0,01€ !), soit à 97,12€ et 105,50€ ? !
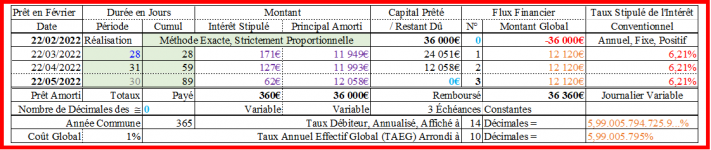
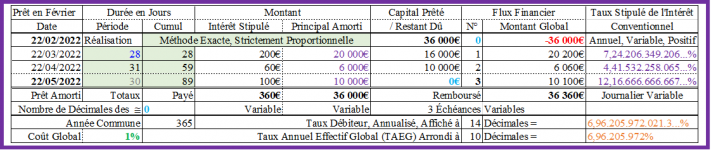
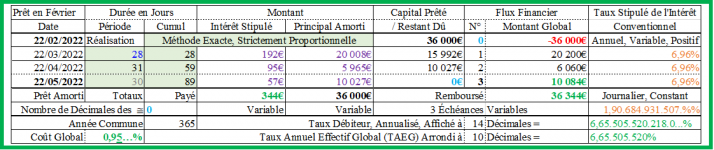
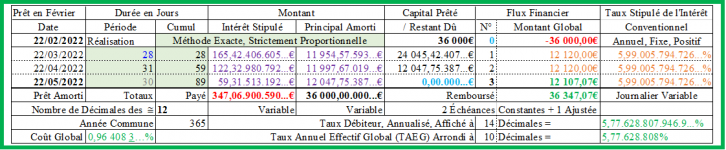
Méthode Exacte (Le remboursement est apériodique ! ...) :
Avec le même taux annuel de l’intérêt conventionnel de 3,5166% et le même montant constant de 12 070,40€ pour les échéances courantes (Hormis donc la dernière, ajustée), si on applique la méthode Exacte, on obtient :
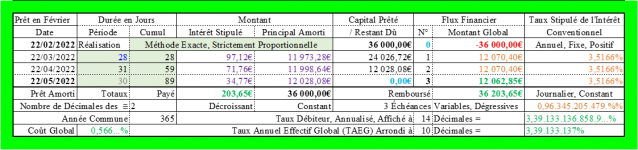
Échéance 1 :
Intérêt : 3,5166%/An / 365Jours/An x 28Jours/Mois x 36 000€ = 97,11 596 712 328 7…€ ≈ 97,12€ ;
Principal amorti : 12 070,40€ - 97,12€ = 11 973,28€ ; CRD : 36 000€ - 11 973,28€ = 24 026,72€ ;
Échéance 2 :
Intérêt : 3,5166%/An / 365Jours/An x 31Jours/Mois x 24 026,72€ = 71,76 063 753 731 506 849…€ ≈ 71,76€ ;
Principal amorti : 12 070,40€ - 71,76€ = 11 998,64€ ; CRD : 24 026,72€ - 11 998,64€ = 12 028,08€ ;
Échéance 3 :
Intérêt : 3,5166%/An / 365Jours/An x 30Jours/Mois x 12 028,08€ = 34,76 543 517 369 863 01…€ ≈ 34,77€ ;
Principal amorti : 12 028,08€ ; CRD : 12 028,08€ - 12 028,08€ = 0€, au terme du prêt ! ;
Taux débiteur annualisé = TAEG : 3,39 133…% ≠< 3,5166% (Taux annuel de l’intérêt conventionnel) !
On voit, alors, que le coût global du prêt n’est plus que de 203,65€ ≠< 211,20€ (Différence : 7,55€ !), que le montant de la dernière échéance est ajusté et n’est plus de 12 070,40€ mais de 12 062,85€ (Différence : 7,55€ !), et que le taux débiteur, égal au TAEG, ne s’élève plus qu’à : 3,3913…% ≠< 3,5166…% :
Différence : 3,5166…% - 3,3913…% = 0,1253…% > 0,1% de tolérance théoriquement admissible ! ...
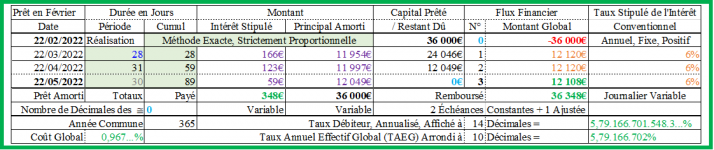
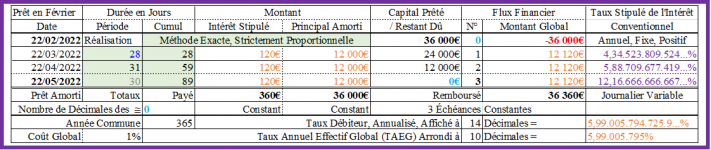
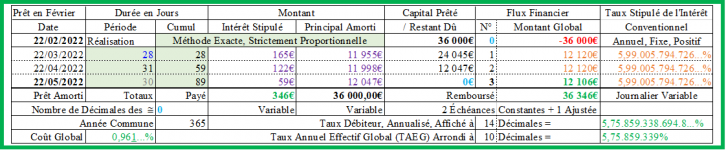
Et si on veut maintenir le montant des échéances constant, à la valeur de 12 070,40€, et donc le coût global du prêt de 211,20€, il convient d’augmenter le taux annuel de l’intérêt conventionnel jusqu’à la valeur, calculée par itération ou par la fonction "Valeur cible" d’EXCEL, de 3,6466% ≠> 3,5166%, comme ci-dessous :
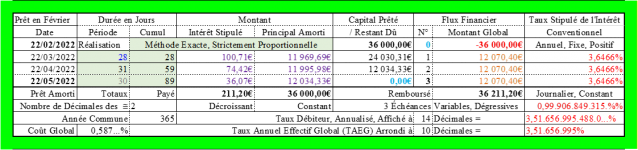
Échéance 1 :
Intérêt : 3,6466%/An / 365Jours/An x 28Jours/Mois x 36 000€ = 100,70 610 410 958 9…€ ≈ 100,71€ ;
Principal amorti : 12 070,40€ - 100,71€ = 11 969,69€ ; CRD : 36 000€ - 11 969,69€ = 24 030,31€ ;
Échéance 2 :
Intérêt : 3,6466%/An / 365Jours/An x 31Jours/Mois x 24 030,31€ = 74,42 456 936 509 589 041…€ ≈ 74,42€ ;
Principal amorti : 12 070,40€ - 74,42€ = 11 995,98€ ; CRD : 24 030,31€ - 11 995,98€ = 12 034,33€ ;
Échéance 3 :
Intérêt : 3,6466%/An / 365Jours/An x 30Jours/Mois x 12 034,33€ = 36,06 935 981 753 424 65…€ ≈ 36,07€ ;
Principal amorti : 12 034,33€ ; CRD : 12 034,33€ - 12 034,33€ = 0€, au terme du prêt ! ;
Taux débiteur annualisé = TAEG : 3,5166…% ≠< 3,6466% (Taux annuel de l’intérêt conventionnel) !
Le taux débiteur est revenu à sa valeur de 3,5166…%, mais pas le taux annuel de l’intérêt conventionnel :
Différence : 3,6466…% - 3,5166…% = 0,13…% > 0,1% de tolérance théoriquement admissible ! ...
Bien entendu, là encore, il n’y a toujours "aucun intérêt" à ne pas arrondir les montants des intérêts mensuels :
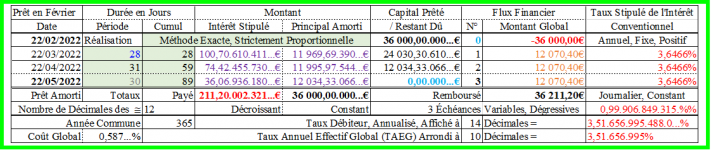
Par comparaison entre les deux méthodes Exacte et du "Mois Normalisé", que l’on arrondisse au centime ou non, on voit bien ici encore que pour un même flux financier de remboursement du prêt, si le taux débiteur, ici égal au TAEG car il n’y a pas de charge annexe, est le même dans les deux cas (3,5166…%), le taux annuel de l’intérêt conventionnel qui permet de calculer les intérêts mensuels n’est pas le même (3,6466% ≠> 3,5166%), ce qui démontre implicitement que le taux débiteur n’est pas systématiquement égal au taux annuel de l’intérêt conventionnel ! :
Ce sont deux entités différentes qui peuvent avoir la même valeur, ou approximativement la même valeur, mais qui, justement, n’ont pas forcément la même valeur ! ...
Cdt.
Bonjour à tous !
Toujours aucune réaction ?
Ni contestation, ni approbation ?
La terreur règne vraiment dans ce forum ! ...
Ou bien, trop compliqué jusqu’ici ? Pourquoi pas ?
Il faudrait simplifier, condenser, se mettre à la portée du Lecteur éventuel !
Revenons à des tableaux d’amortissement moins longs, plus faciles à analyser : 3 échéances devraient suffire ;
Et puis, tant qu’on y est, un taux annuel de l’intérêt conventionnel, stipulé et fixé par écrit, constant (Ça ira ?)
Reprenons donc le prêt, rappelé le vendredi 07/01/2022, d’un capital de 36 000€, emprunté le 22/02/2022, assorti d’un intérêt global stipulé de 211,20€, toujours remboursé mensuellement, les 22/03/2022, 22/04/2022 et 22/05/2022, mai cette fois, par échéances de montant constant (36 211,20€ / 3M = 12 070,40€), avec un taux annuel de l’intérêt conventionnel, déterminé pour cela, à 3,5166%, par calcul itératif ou par la fonction "Valeur cible" d’EXCEL par exemple, et dont le tableau d’amortissement est le suivant :
Méthode dite du "Mois Normalisé" (Le remboursement est pseudopériodique ! ...) :

Échéance 1 :
Intérêt : 3,5166%/An / 12Mois/An x 36 000€ = 105,49 8€ ≈ 105,50€ ;
Principal amorti : 12 070,40€ - 105,50€ = 11 964,90€ ; CRD : 36 000€ - 11 964,90€ = 24 035,10€.
Échéance 2 :
Intérêt : 3,5166%/An / 12Mois/An x 24 035,10€ = 70,43 486 055€ ≈ 70,43€ ;
Principal amorti : 12 070,40€ - 70,43€ = 11 999,97€ ; CRD : 24 035,10€ - 11 999,97€ = 12 035,13€.
Échéance 3 :
Intérêt : 3,5166%/An / 12Mois/An x 12 035,13€ = 35,26 894 846 5€ ≈ 35,27€ ;
Principal amorti : 12 035,13€ ; CRD : 12 035,13€ - 12 035,13€ = 0€, au terme du prêt !
Taux débiteur annualisé = TAEG : 3,51 656 995…% ≈ 3,5166% (Taux annuel de l’intérêt conventionnel) : OK !
Évidemment, ces calculs et cette démonstration ne venant pas de lui, Aristide qui pense être le seul à détenir la vérité, pourra toujours contester virulemment ce qui est écrit ci-dessus, au prétexte que des calculs doivent être exacts et que, du coup, d’après lui, il ne faut surtout pas arrondir les montants mensuels des intérêts !
Même s’il se gardera d’afficher tous les chiffres significatifs au-delà des centimes, pour lui, le véritable tableau d’amortissement devrait, sans doute, être celui-ci ! :

Là, c’est sûr, avec cette théorie "fumeuse" et un flux financier strictement identique, d'où un même coût du prêt, égal, ici, au montant global de l'intérêt stipulé, et strictement les mêmes TAEG et taux débiteur, nous voilà bien avancés !
Et quand on sait que par la méthode Exacte ci-après, le montant des intérêts de la première échéance, sans arrondi au centime, s’élève à 97,11 596 712 328 7…€ ≠< 105,498€ ;
La différence étant de 105,49 8€ - 97,11 596 712 328 7…€ = 8,38 203 287 671 2…€ ≈ 8,38…€ ;
On se demande bien à quoi rimerait de ne pas arrondir les montants respectifs à un "pauvre" centime (0,01€ !), soit à 97,12€ et 105,50€ ? !
Méthode Exacte (Le remboursement est apériodique ! ...) :
Avec le même taux annuel de l’intérêt conventionnel de 3,5166% et le même montant constant de 12 070,40€ pour les échéances courantes (Hormis donc la dernière, ajustée), si on applique la méthode Exacte, on obtient :

Échéance 1 :
Intérêt : 3,5166%/An / 365Jours/An x 28Jours/Mois x 36 000€ = 97,11 596 712 328 7…€ ≈ 97,12€ ;
Principal amorti : 12 070,40€ - 97,12€ = 11 973,28€ ; CRD : 36 000€ - 11 973,28€ = 24 026,72€ ;
Échéance 2 :
Intérêt : 3,5166%/An / 365Jours/An x 31Jours/Mois x 24 026,72€ = 71,76 063 753 731 506 849…€ ≈ 71,76€ ;
Principal amorti : 12 070,40€ - 71,76€ = 11 998,64€ ; CRD : 24 026,72€ - 11 998,64€ = 12 028,08€ ;
Échéance 3 :
Intérêt : 3,5166%/An / 365Jours/An x 30Jours/Mois x 12 028,08€ = 34,76 543 517 369 863 01…€ ≈ 34,77€ ;
Principal amorti : 12 028,08€ ; CRD : 12 028,08€ - 12 028,08€ = 0€, au terme du prêt ! ;
Taux débiteur annualisé = TAEG : 3,39 133…% ≠< 3,5166% (Taux annuel de l’intérêt conventionnel) !
On voit, alors, que le coût global du prêt n’est plus que de 203,65€ ≠< 211,20€ (Différence : 7,55€ !), que le montant de la dernière échéance est ajusté et n’est plus de 12 070,40€ mais de 12 062,85€ (Différence : 7,55€ !), et que le taux débiteur, égal au TAEG, ne s’élève plus qu’à : 3,3913…% ≠< 3,5166…% :
Différence : 3,5166…% - 3,3913…% = 0,1253…% > 0,1% de tolérance théoriquement admissible ! ...
Et si on veut maintenir le montant des échéances constant, à la valeur de 12 070,40€, et donc le coût global du prêt de 211,20€, il convient d’augmenter le taux annuel de l’intérêt conventionnel jusqu’à la valeur, calculée par itération ou par la fonction "Valeur cible" d’EXCEL, de 3,6466% ≠> 3,5166%, comme ci-dessous :

Échéance 1 :
Intérêt : 3,6466%/An / 365Jours/An x 28Jours/Mois x 36 000€ = 100,70 610 410 958 9…€ ≈ 100,71€ ;
Principal amorti : 12 070,40€ - 100,71€ = 11 969,69€ ; CRD : 36 000€ - 11 969,69€ = 24 030,31€ ;
Échéance 2 :
Intérêt : 3,6466%/An / 365Jours/An x 31Jours/Mois x 24 030,31€ = 74,42 456 936 509 589 041…€ ≈ 74,42€ ;
Principal amorti : 12 070,40€ - 74,42€ = 11 995,98€ ; CRD : 24 030,31€ - 11 995,98€ = 12 034,33€ ;
Échéance 3 :
Intérêt : 3,6466%/An / 365Jours/An x 30Jours/Mois x 12 034,33€ = 36,06 935 981 753 424 65…€ ≈ 36,07€ ;
Principal amorti : 12 034,33€ ; CRD : 12 034,33€ - 12 034,33€ = 0€, au terme du prêt ! ;
Taux débiteur annualisé = TAEG : 3,5166…% ≠< 3,6466% (Taux annuel de l’intérêt conventionnel) !
Le taux débiteur est revenu à sa valeur de 3,5166…%, mais pas le taux annuel de l’intérêt conventionnel :
Différence : 3,6466…% - 3,5166…% = 0,13…% > 0,1% de tolérance théoriquement admissible ! ...
Bien entendu, là encore, il n’y a toujours "aucun intérêt" à ne pas arrondir les montants des intérêts mensuels :

Par comparaison entre les deux méthodes Exacte et du "Mois Normalisé", que l’on arrondisse au centime ou non, on voit bien ici encore que pour un même flux financier de remboursement du prêt, si le taux débiteur, ici égal au TAEG car il n’y a pas de charge annexe, est le même dans les deux cas (3,5166…%), le taux annuel de l’intérêt conventionnel qui permet de calculer les intérêts mensuels n’est pas le même (3,6466% ≠> 3,5166%), ce qui démontre implicitement que le taux débiteur n’est pas systématiquement égal au taux annuel de l’intérêt conventionnel ! :
Ce sont deux entités différentes qui peuvent avoir la même valeur, ou approximativement la même valeur, mais qui, justement, n’ont pas forcément la même valeur ! ...
Cdt.
Dernière modification: