Bonjour,
attente92 a dit:
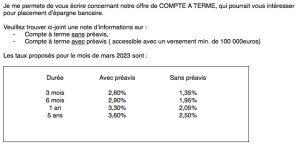
en plus , attention avec la simulation taux actuariel 3% mais taux nominal de 2.9583% . 30 k euros rapportent 887.49 euros
au lieu de 900 euros avec méthode des intérêts simples donc perte d'intérêts de 12.51 euros.
Boursorama ne rémunère que 360 jours les fonds et non pas 365 jours .
887.49= 30 k euros *((1+3%)^(360/365)-1)). Pas cool.
Vous avez bien raison de dire « Pas cool. »
Mais avant d’expliquer cela j’en profite pour préciser/rectifier ce que vous écrivez :
« taux actuariel 3% mais taux nominal de 2.9583% »
En effet vous opposez un « taux actuariel » et « un taux nominal » ; c’est un peu la même chose que si vous compariez « un choux et une carotte ».
En réalité :
+ Un « Taux actuariel » s’oppose à un « Taux proportionnel»
Et
+ Un « Taux Nominal » s’oppose à un « Taux Effectif »
=> Si bien que l’on a à la fois :
+ Un « Taux Nominal Actuariel » et un « Taux Nominal proportionnel »
+ Un « Taux Effectif Actuariel » (c’est un TAEG) et un « Taux Effectif proportionnel » (c’est un TEG).
=> Un taux Nominal se calcule par rapport au montant brut placé (= épargne) ou au montant brut prêté (= crédit)
=> Un taux Effectif se calcule par rapport au montant net placé (= épargne - frais initiaux) ou au montant net prêté (= crédit - frais initiaux).
À noter que, depuis un décret de 2016 concernant les crédits, l’appellation « taux nominal » a été remplacée par « Taux débiteur »
Et, par assimilation, le taux nominal d’un produit d’épargne peut aussi être appelé « Taux créditeur ».
Quant à la notion de taux actuariel elle repose sur la fréquence de la capitalisation des intérêts
+ Inférieure à l’année (jours - mois - trimestre - semestre)
+ Égale à l’année
+ Supérieure à l’année
+ Pour une capitalisation des intérêts à une
périodicité inférieure à l’année, le taux actuariel sera
supérieur au taux proportionnel,
+ Pour une capitalisation des intérêts à une
périodicité égale à l’année, le taux actuariel sera
égal au taux proportionnel,
+ Pour une capitalisation des intérêts à une
périodicité supérieure à l’année, le taux actuariel sera
inférieur au taux proportionnel.
+ Plus la périodicité de capitalisation est grande plus le taux actuariel est élevé et inversement.
=> Des exemples concrets vont sans doute permettre de mieux comprendre :
Supposons donc un produit d’épargne au « taux nominal proportionnel » de 3%
l’an (
l’an = c’est ainsi qu’un taux doit être exprimé dans la réglementation française)
+ Si la capitalisation des intérêts est
mensuelle le « taux équivalent mensuel » sera égal à 3%/12 = 0,25%
Et le taux « nominal actuariel sera [((1+0,25%)^(12)) - 1] =
3,041595691%.....donc bien supérieur au « taux « nominal proportionnel » de 3%.
+ Si la capitalisation des intérêts est
semestrielle le « taux équivalent semestriel » sera égal à 3%/2 = 1,50%
Et le taux « nominal actuariel sera [((1+1,50%)^(2)) - 1] =
3,0225%.....donc bien
supérieur au « taux « nominal proportionnel » de 3%........mais
inférieure au « taux nominal actuariel » en capitalisation mensuelle
+ Si la capitalisation des intérêts est
annuelle le « taux équivalent annuel » sera égal à 3%/1 = 3%.
Et le taux « nominal actuariel sera [((1+3%)^(1)) - 1] =
3,00%.....donc bien
égal au « taux « nominal proportionnel » de 3%.
+ Si la capitalisation des intérêts est
bisannuel/biennal le « taux équivalent bisannuel » sera égal à 3%/(1/2) = 6%.
Et le taux « nominal actuariel sera [((1+6%)^(1/2)) - 1] =
2,956301%.....donc bien
inférieur au « taux « nominal proportionnel » de 3%.
Venons-en maintenant au sujet de ce post :
en plus , attention avec la simulation taux actuariel 3% mais taux nominal de 2.9583% . 30 k euros rapportent 887.49 euros au lieu de 900 euros avec méthode des intérêts simples donc perte d'intérêts de 12.51 euros.
Boursorama ne rémunère que 360 jours les fonds et non pas 365 jours .
887.49= 30 k euros *((1+3%)^(360/365)-1)). Pas cool.
+ Si 30.000€ étaient placés au taux de 3% l’an avec une seule capitalisation annuelle, ainsi qu’expliqué antérieurement le « Taux nominal proportionnel » serait strictement identique au « Taux nominal actuariel » et serait donc tous les deux de 3%
+ Dès lors le montant des intérêts capitalisés au bout d’un an devrait être :
= 30.000€ x 3% = 900€ tous ronds.
Or par une manœuvre cette banque vous calcule les intérêts ainsi :
= 30.000€ x 3% / 365 x 360 =
887,67€……….ET NON PAS 887,49 euros ???
Non seulement elle vous trompe sur le nombre de jours mais en plus
il manque encore 0,18 € ???
Mais - quel que soit le nombre de jours considérés - il n’y a bien qu’une capitalisation annuelle.
Le « taux nominal proportionnel » de votre placement est donc de :
= 887,49€/30.000€ x 100 = 2,9583%
Mais ainsi que je l’ai expliqué ci-dessus en supposant une capitalisation à 360 jours cela signifie que la périodicité de capitalisation est inférieure à l’année et qu’il y aurait 365/360 = 1,01388888…capitalisations dans ladite année.
Suivant ce que j’ai expliqué antérieurement le « taux nominal actuariel » devrait donc être :
+ Le « taux équivalent périodique » sera égal à 3%/(365/360) = 2,95890411%
Et le taux « nominal actuariel sera [((1+(3%/(365/360))^(365/360)) - 1] =
3,00061053%.....donc bien supérieur au « taux « nominal proportionnel » de 3%.
Edit
Suite à la remarque de Jodel140 j'ai supprimé mon commentaire sévère.
Mais le taux actuariel n'est cependant pas de 3%; si l'on suppose un terme à 360 jours (et non pas à 12 mois) le replacement immédiat du capital et des intérêts donnerait un taux actuariel de 3,00061% ansi que calculé ci-dessus.
Cdt
