Les actions américaines

[D-Jack]

Et eux payent leur santé

Vous aussi, du moins partiellement

 

[mvhrb888]

il faut pas oublier le coup de la vie

Pas mal, le coup de la vie ! En tout cas mieux qu’un coup mortel

Alors, justement, tous ces chiffres sur les salaires, ce sont les salaires bruts ou nets ? Avant de payer son assurance santé ou après ?

 

[Max1]

Et eux payent leur santé

Quand je vois les prélèvements sur mon salaire chaque mois, j'ai pas l'impression que se soit gratuit ici non plus.
Pour ce qui est du coût des études, on n'a vraiment pas à se plaindre. On ne nous demande pas de payer 20-30k par an rien qu'en frais d'inscriptions.

 

[Max1]

Alors, justement, tous ces chiffres sur les salaires, ce sont les salaires bruts ou nets ? Avant de payer son assurance santé ou après ?

Dans les grosses boîtes, c'est souvent proposé comme un avantage salarial payé directement par la boîte et ils peuvent même choisir entre plusieurs formules. (Nous on reçoit des tickets resto ou une voiture de fonction ou un abonnement aux transports publics, eux ils reçoivent une assurance ;-) ).
Par contre, je ne sais pas non plus si c'est pris en compte dans ces statistiques.

 

[polo88]

Des chiffres prix de façon brute comme ça non pas vraiment de sens dans la vie.
Il faut comparer ce qui est comparable il y a tellement de facteurs influents et de billets qu'il est difficile de conclure sur ces chiffres effectivement.
La vie n'est pas la même dans les deux pays les frais non plus les droits non plus...
Il faudrait prendre le salaire effectivement et en déduire les frais obligatoires et voir ce qu'il reste à la fin c'est un peu comme ça qu'on fait chacun ses comptes je crois

 

[Jeune_padawan]

Alors, justement, tous ces chiffres sur les salaires, ce sont les salaires bruts ou nets ?

Brut, avant les charges (oui oui il y a des charges salariales et patronales aux États-Unis notamment pour financer le système Medicare et Medicaid).

Pour revenir au sujet initial, c'est la définition, par l'INSEE et les grands instituts de statistiques, de classe moyenne qui peut surprendre :

La classe moyenne est définie comme l’ensemble des ménages dont le revenu avant impôts est compris entre deux tiers et deux fois le revenu médian.

Vous voyez beaucoup

Mon clavier était en grève

La vie n'est pas la même dans les deux pays les frais non plus les droits non plus...

Les États-Unis sont libéraux sauf pour le commerce extérieur, pays de la libre entreprise.
La France est vue comme un pays socialist (ce qui équivaut à communiste dans le langage américain) avec son système social.

Pour ce qui est des droits, les français devraient arrêter de regarder leur nombril et regarder un peu ailleurs avant de râler. Ne pas oublier qu'un droit essentiel a été retiré récemment aux américaines...

 

[steph12002]

Bonjour,

le graphique ci-dessous (cours SP 500) ne vous alerte pas un peu ? Depuis 2009, ça monte sec ! On a été depuis 2009 sous perfusion de liquidités, la remontée des taux, la fermeté des banques centrales, etc. a peut-être mis fin à cette période faste pour les actions (et la gestion passive par ETF SP 500) ? On nous fait croire que la recette miracle avec des gagnants certains serait d'investir en DCA sur un ETF SP 500 sur une longue période. Je ne suis pas tellement convaincu qu'en investissant aujourd'hui on soit gagnant en 2042.

 

[sorcier]

Je ne suis pas tellement convaincu qu'en investissant aujourd'hui on soit gagnant en 2042.

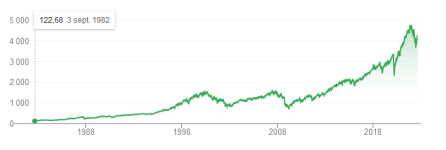
Pour moi tout dépend de si tu continues à investir ou pas et si tu n'utilises que de l'argent dont tu n'as pas besoin.

Je me suis pris la crise de 2000 investi à 100% (et sans ETFs à l'époque). J'étais dégouté. J'ai même fermé mon PEA... Bien sûr en perdant un max.

Si j'avais continue aveuglement j'aurais une vraie fortune aujourd'hui...

Maintenant je n’arrête pas d'investir peu à peu, mais j'attends le S&P à 3600 pour prendre un peu plus, à 3300 pour renforcer et à 3000 pour me gaver.

 

[sorcier]

Je ne suis pas tellement convaincu qu'en investissant aujourd'hui on soit gagnant en 2042.

Il faut prendre en compte l'inflation pour voir où on est. Je n'ai pas trouvé que des données allant jusqu'à 2014

 

[steph12002]

Merci sorcier pour ton retour d'expérience

 

[Jeune_padawan]

le graphique ci-dessous (cours SP 500) ne vous alerte pas un peu ?

C'est mieux en échelle logarithmique :

Il faut prendre en compte l'inflation pour voir où on est. Je n'ai pas trouvé que des données allant jusqu'à 2014

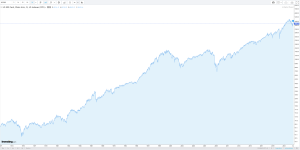
On peut rajouter les dividendes également car les ETF les capitalisent ou bien les redistribuent.

S&P 500 :


S&P 500 Total Return (dividendes réinvestis brut) :


S&P 500 Net Total Return (dividendes réinvestis net de prélèvement à la source US) :



Méthodologie du S&P 500 et des version TR et NTR (page notée 19) : [lien réservé abonné]

 

[steph12002]

C'est mieux en échelle logarithmique :

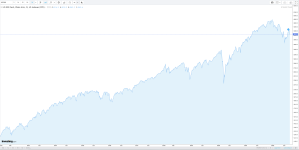
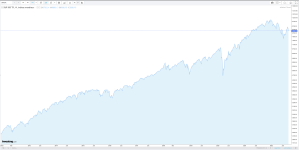
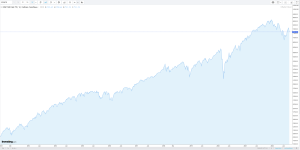
Jeune_padawan, pourquoi prendre en échelle logarithmique, c'est biaiser les données, non ? Merci

 

[Jeune_padawan]

pourquoi prendre en échelle logarithmique, c'est biaiser les données, non ?

Non au contraire, cette échelle clarifie les données car elle permet de conserver les proportions dans le temps en affichant les variations en % du cours précédent. En gros l'echelle permet de relativiser les variations dans le temps.

Surtout cela montre que malgré le fait que les marchés se soient gavés avec les QE FED/BCE, la progression est plus linéaire que ce que les pseudo-expert boursier sur internet peuvent dire.

 

[sorcier]

Surtout cela montre que malgré le fait que les marchés se soient gavés avec les QE FED/BCE, la progression est plus linéaire que ce que les pseudo-expert boursier sur internet peuvent dire.

Plus exponentielle serait un meilleur mot.

 

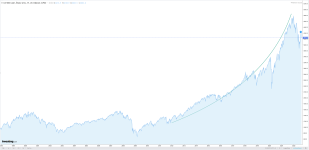
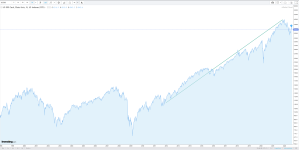
[Jeune_padawan]

Plus exponentielle serait un meilleur mot.

Plus exponentielle en échelle linéaire :


Et plus linéaire en échelle logarithmique :

 

[sorcier]

Plus exponentielle en échelle linéaire :

Tu ne m'as pas compris. Une droite en échelle logarithmique représente une courbe exponentielle.

Ce que tu peux visualiser facilement en mettant l'échelle logarithmique est si la progression est en train de s’accélérer ou pas, mais la progression elle même représente une courbe exponentielle indépendamment de l'échelle choisie.

 

[Jeune_padawan]

Tu ne m'as pas compris. Une droite en échelle logarithmique représente une courbe exponentielle.

je viens de comprendre en posant une opération fictive type ln(exp(x)).

 

[Jeune_padawan]

Ce que tu peux visualiser facilement en mettant l'échelle logarithmique est si la progression est en train de s’accélérer ou pas, mais la progression elle même représente une courbe exponentielle indépendamment de l'échelle choisie.

Ah oui effectivement en calculant le coefficient de proportionnalité de la droite issue de la transformation de l'exponentielle (via passage en échelle logarithmique) on peut mesurer l’accélération de la progression. Mais je ne pousse pas à ce point là mes mesures.

 

[sorcier]

Ah oui effectivement en calculant le coefficient de proportionnalité de la droite issue de la transformation de l'exponentielle (via passage en échelle logarithmique) on peut mesurer l’accélération de la progression. Mais je ne pousse pas à ce point là mes mesures.

C'est la beauté de la représentation logarithmique. Plus forte est la pente, plus forte est la progression et vice-versa. La chose importante est regarder les changements de pente de la droite en échelle log.

 

[steph12002]

Non au contraire, cette échelle clarifie les données car elle permet de conserver les proportions dans le temps en affichant les variations en % du cours précédent. En gros l'echelle permet de relativiser les variations dans le temps.

Surtout cela montre que malgré le fait que les marchés se soient gavés avec les QE FED/BCE, la progression est plus linéaire que ce que les pseudo-expert boursier sur internet peuvent dire.

Merci Jeune_padawan (bien que je ne sois pas totalement convaincu)