zyxel
Contributeur régulier
Vous parlez de la France ou de l'Argentine ?Jeune_padawan a dit:Notation CCC, instabilité économique et politique 15% de YTM c'est plus un pari c'est un grain de folie pour le fun et l'adrénaline.


Suivez la vidéo ci-dessous pour voir comment installer notre site en tant qu'application web sur votre écran d'accueil.
Note.: Cette fonctionnalité peut ne pas être disponible dans certains navigateurs.
Vous parlez de la France ou de l'Argentine ?Jeune_padawan a dit:Notation CCC, instabilité économique et politique 15% de YTM c'est plus un pari c'est un grain de folie pour le fun et l'adrénaline.


La France malgré sa 5ème colonne interne n'en ai pas encore à ce stade de dégradation. Quoique qu'on lise sur ce forum, l'inflation rentre dans le rang, l'économie fonctionne. Le hic est possiblement du coté de la dépense publique et de l'efficacité des services publiques.zyxel a dit:Vous parlez de la France ou de l'Argentine ?
Oui, mais les USA ont le.. Dollar !Jeune_padawan a dit:La France malgré sa 5ème colonne interne n'en ai pas encore à ce stade de dégradation. Quoique qu'on lise sur ce forum, l'inflation rentre dans le rang, l'économie fonctionne. Le hic est possiblement du coté de la dépense publique et de l'efficacité des services publiques.
Et pour rappel la France n'a pas fait défaut depuis 1797 (Tiers consolidé) alors que que les États-Unis ont fait défaut en 1933.
$ ou pas $, si personne ne veut plus prêter ils l'ont dans l'os.zyxel a dit:Oui, mais les USA ont le.. Dollar !
Bonjour,Greg42 a dit:bonjour
chez fortuneo , ils indiquent une echéance en 2054 pour la AXA...
ExactGreg42 a dit:depuis 20 ans AXA a toujours versé un dividende non ?
4 + 22% x 3 = 4.66 ce qui fait environ 4.8% sur le prix actuel de l'obligation.Greg42 a dit:en l'achetant aujourd'hui à 97.34% ça donne 4.11% de rendement minimum (si versement coupon maintenu evidemment) et 6.81% au taux actuel du cms 10ans
c'est bien ça ?
Oui et non, comme il y a une composante variable, indexée sur le taux interbancaire à 10 ans, ça diminue un peu la sensibilité taux.Greg42 a dit:d'autre part l'echéance étant très lointaine , c'est une obligation très sensible aux taux ?
AUTRE QUESTIONPhil17000 a dit:Bonjour,
Selon les sites, ils mettent différentes dates. J'ai notamment vu du 2099. Mais c'est bien une perpétuelle rappelable au gré de l'émetteur et la prochaine date de rappel potentiel est en avril 2025.
Exact
4 + 22% x 3 = 4.66 ce qui fait environ 4.8% sur le prix actuel de l'obligation.
Oui et non, comme il y a une composante variable, indexée sur le taux interbancaire à 10 ans, ça diminue un peu la sensibilité taux.
C'est une obligation zéro-coupon. Vous toucherez à l'échéance les intérêts cumulés en même temps que le remboursement du capital.Greg42 a dit:AUTRE QUESTION
concernant
CREDIT AGRICOLE 0% 09/05/31 EUR [lien réservé abonné]
FRCASA010084
le cours est à 100.37 pour un prix d'émission de 99.26%
quel est l'interet d'acheter une telle obligation ?
vu que coupon 0 et au dessus du pair...
comment boursorama trouve 4.03% de taux actuariel ?
en fait c'est 4% zero coupon et pas 0%Phil17000 a dit:C'est une obligation zéro-coupon. Vous toucherez à l'échéance les intérêts cumulés en même temps que le remboursement du capital.
Oui c'est le rendement des obligations CASA en général.Greg42 a dit:en fait c'est 4% zero coupon et pas 0%
Bonjour,Greg42 a dit:j'ai trouvé CASA1.5% 27OCT30
en arrivant à l'acheter à 84.77% j'arrive à un yield de 4.14%
si je n'ai pas fait d'erreur
il reste en gros 77 mois , le retour au pair rapportera 15.23% (100-84.77)
soit 2.37% par an
je calcul un coupon annuel ( alors qu'il est trimestriel donc je sous evalue le rendement) de 1.5% sur 84.77% soit 1.77% par an
2.37+1.77= 4.14%
si quelqu'un a la bonté de me confirmer que j'ai juste
merci
bonjourApprentiEpargnant a dit:Bonjour,
Votre rendement global pour le retour au pair est de 17,97% (100-84.77)/84.77 (non pas 15.23)
Vous obtenez un rendement annualisé de ((1+0.1797)^(1/6.42))-1 = 2.61%
(6.42 c'est le nombre d'années restantes 77/12)
Pour le coupon, vous allez recevoir 1.5€*6.42 soit 9.63€
Ce qui vous donne un rendement global de 11.36%
Vous obtenez un rendement annualisé de ((1+0.1136)^(1/6.42))-1 = 1.69%
Pour le rendement global,
Vous gagnez 15.23€ de retour au pair et 9.63€ de coupons soit 24.86€
Rendement global de 24.86/84.77 = 29.33%
Rendement annualisé de ((1+0.2933)^(1/6.42))-1 = 4.09%
Parce que les intérêts se composent.Greg42 a dit:bonjour
merci beaucoup d'avoir pris le temps de m'expliquer en détail
chui pas encore tout à fait au point...
par contre , comment se fait il que la somme de vos 2 rendements annualisés 1.69 + 2.61
ne fasse pas 4.09 comment vous trouvez en bas mais 4.3 ?
encore merci
Merci @ApprentiEpargnant pour l'exerciceApprentiEpargnant a dit:Bonjour,
Votre rendement global pour le retour au pair est de 17,97% (100-84.77)/84.77 (non pas 15.23)
Vous obtenez un rendement annualisé de ((1+0.1797)^(1/6.42))-1 = 2.61%
(6.42 c'est le nombre d'années restantes 77/12)


Il faut capitaliser les coupons puisqu'ils sont versés au fil de l'eau.ApprentiEpargnant a dit:Pour le coupon, vous allez recevoir 1.5€*6.42 soit 9.63€
Ce qui vous donne un rendement global de 11.36%
Vous obtenez un rendement annualisé de ((1+0.1136)^(1/6.42))-1 = 1.69%
Avec les modifications ci-dessus, je trouve 4.41% mais Bloomberg 4.32%ApprentiEpargnant a dit:Pour le rendement global,
Vous gagnez 15.23€ de retour au pair et 9.63€ de coupons soit 24.86€
Rendement global de 24.86/84.77 = 29.33%
Rendement annualisé de ((1+0.2933)^(1/6.42))-1 = 4.09%
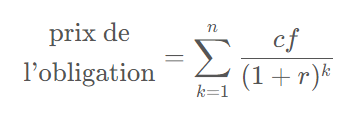


OuiApprentiEpargnant a dit:Je pense qu'@Aristide devrait nous fournir une réponse plus proche que toi ou moi. ;-)
Edit: Il a déjà répondu en fait.

Pour un calcul exact cette équation ne convient pas avec des flux de trésorerie qui ne sont pas annuels ou/et pas à périodicité régulière.ApprentiEpargnant a dit:Ce qui fait que tu dois poser
1.5/(1+r)^1 + 1.5/(1+r)^2 + .... = 84.772
Aristide a dit:Bonjour,
En "grappillant" de-ci de-là les données approximatives fournies par les uns et les autres je trouve un taux de rentabilité actuariel de 4,29% après arrondi à deux décimales au plus proche.
Ci-joint tableau Excel avec méthode adéquate.
Il est à penser qu'en la reprenant avec les données exactes l'on retrouverait les 4,32% ci-dessus évoqués.
A toutes fins utiles.
Cdt
Top !ApprentiEpargnant a dit:Bonjour @Phil17000,
Je n'utilise pas la formule des intérêts composés car même si l'on reçoit bien le coupon tous les ans il n'est pas réinvesti dans l'obligation, et même s'il l'est, il ne le sera pas forcément au même rendement donc cela compliquera encore plus le calcul. Je sais que je fais un raccourci, mais je préfère calculer de cette façon (rendement in-fine).
De la même manière que l'on a zappé que le versement du coupon était trimestriel, ce qui normalement augmente très légèrement ton rendement par rapport à un versement annuel comme calculé. (La différence est minime vu le coupon et la duration de l'obligation).
Si tu veux retomber sur le YTM de ton terminal Bloomberg (d'ailleurs tu me dis quand tu le jettes hein!) il faut créer l'itération de la formule des flux de trésorerie. Et encore, avec la formule ci-dessous, tu ne peut que compter en années pleines...
Nous avons toutes les données, ce que l'on souhaite c'est le petit r.
Afficher la pièce jointe 29442
Ce qui fait que tu dois poser
1.5/(1+r)^1 + 1.5/(1+r)^2 + .... = 84.772
Pour info YTM pour 6 ans est de 4.45% et pour 7 ans de 4.04% en comptant un versement annuel
Je te laisse revenir vers nous pour 6.42 années. Tu as deux heures!
Je pense qu'@Aristide devrait nous fournir une réponse plus proche que toi ou moi. ;-)
Edit: Il a déjà répondu en fait.
BonjourAristide a dit:Bonjour,
En "grappillant" de-ci de-là les données approximatives fournies par les uns et les autres je trouve un taux de rentabilité actuariel de 4,29% après arrondi à deux décimales au plus proche.
Ci-joint tableau Excel avec méthode adéquate.
Il est à penser qu'en la reprenant avec les données exactes l'on retrouverait les 4,32% ci-dessus évoqués.
A toutes fins utiles.
Cdt
Aristide a dit:Oui
Pour un calcul exact cette équation ne convient pas avec des flux de trésorerie qui ne sont pas annuels ou/et pas à périodicité régulière.
Cdt
 Aspa : les nouveaux seuils 2026 pour rembourser à l'Etat le minimum vieillesse en cas de décès
Aspa : les nouveaux seuils 2026 pour rembourser à l'Etat le minimum vieillesse en cas de décès
 CAF : bientôt la fin du RSA, des APL et de la prime d'activité au profit d'une allocation unique ?
CAF : bientôt la fin du RSA, des APL et de la prime d'activité au profit d'une allocation unique ?
 Ces comptes à terme sans risque battent toujours le nouveau taux du Livret A
Ces comptes à terme sans risque battent toujours le nouveau taux du Livret A
 Particuliers employeurs : Smic, Cesu, Pajemploi, tout ce qui change pour votre budget
Particuliers employeurs : Smic, Cesu, Pajemploi, tout ce qui change pour votre budget
 Société Générale (180 €), BNP Paribas (270 €) : la liste des bonus en mars pour l'ouverture d'un compte
Société Générale (180 €), BNP Paribas (270 €) : la liste des bonus en mars pour l'ouverture d'un compte
 Facture de gaz : une hausse à partir du 1er mai pour 60% des particuliers, êtes-vous concerné ?
Facture de gaz : une hausse à partir du 1er mai pour 60% des particuliers, êtes-vous concerné ?


