agra07
Contributeur régulier
L'effet d'aubaine, c'est la somme que peut rapporter cette erreur.LatinGrec a dit:la nullité de la stipulation d'intérêt n'est pas un effet d'aubaine : là est le parti pris
Suivez la vidéo ci-dessous pour voir comment installer notre site en tant qu'application web sur votre écran d'accueil.
Note.: Cette fonctionnalité peut ne pas être disponible dans certains navigateurs.
L'effet d'aubaine, c'est la somme que peut rapporter cette erreur.LatinGrec a dit:la nullité de la stipulation d'intérêt n'est pas un effet d'aubaine : là est le parti pris





Aristide a dit:Oui; mais ainsi que je l'ai expliqué l'arrondi monétaire n'impacte que l'échéance et pas du tout la partie "intérêts" comprise dans ladite échéance.
Il en résulte que - ligne par ligne = échéance par échéance - le taux nominal contractuel est toujours respecté à moins que la banque procède à un arrondi "au supérieur" sur ces intérêts ce qui, à mon avis, ne devrait pas exister (=> pas d'arrondi du tout sur les intérêts ou arrondi à "l'inférieur")
Et si c'est l'échéance qui est impactée seul le TRI (=Taux d'ensemble équivalent au TEG sans aucun frais) s'en trouve aussi impacté.
Suivant les cas il peut être supérieur ou inférieur au taux nominal contractuel mais ce n'est pas ce TRI qui compte; c'est le taux calculé ligne par ligne (Cf jugements tribunaux)
Par ailleurs il en est exactement de même pour une échéance constante adaptée dans un calcul d'intérêts avec la méthode "Exact/Exact" ainsi que le montre l'exemple du fichier Excel joint.
L'on y voit bien qu'avec le calcul "Exact/Exact" la mensualité est légèrement supérieure à celle d'un calcul classique avec le mois normalisé et donc le volume des intérêts payés également.
Mais l'on voit aussi que - ligne par ligne - le taux nominal proportionnel contractuel est strictement respecté cependant que - au contraire - le TRI dépasse le taux nominal proportionnel à partir de la troisième décimale.
Cdt
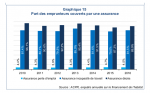
LatinGrec a dit:une brisée lombarde, selon qu'elle soit de moins d'une semaine ou de plus de trois semaines, génère une majoration du taux nominal de l'ordre de 10^-3 à 10^-4 point.
je prendrai volontiers l'avis d'Aristide sur le sujet.
 ) que, dans le cas le plus général, c'est la pratique de l'amortissement figé qui est utilisée et qu'il n'y a donc pas d'effet boule de neige contrairement à ce qui se passe dans les cas d'exception où c'est celle des échéances figées qui et utilisée; seule la première échéance brisée est donc impactée:
) que, dans le cas le plus général, c'est la pratique de l'amortissement figé qui est utilisée et qu'il n'y a donc pas d'effet boule de neige contrairement à ce qui se passe dans les cas d'exception où c'est celle des échéances figées qui et utilisée; seule la première échéance brisée est donc impactée:en retenant une majoration moyenne de + 0.0015 point (totalement arbitraire de ma part) du taux nominal, sur un encours de 900 milliards, l'aubaine lombarde de 0.0015 % est de l'ordre de 13 millions 500 milles €.
Dans mon évaluation, j'ai considéré l'encours en avril 2017 qui est de 250 milliards € si ma vue ne me trahit pas.LatinGrec a dit:Sous le poncif "chacun faire dire aux chiffres ce qu'il veut", voici ce que je veux faire dire aux chiffres :
une brisée lombarde, selon qu'elle soit de moins d'une semaine ou de plus de trois semaines, génère une majoration du taux nominal de l'ordre de 10^-3 à 10^-4 point.
en retenant une majoration moyenne de + 0.0015 point (totalement arbitraire de ma part) du taux nominal, sur un encours de 900 milliards, l'aubaine lombarde de 0.0015 % est de l'ordre de 13 millions 500 milles €.
je prendrai volontiers l'avis d'Aristide sur le sujet.
agra07 a dit:Dans mon évaluation, j'ai considéré l'encours en avril 2017 qui est de 250 milliards € si ma vue ne me trahit pas.
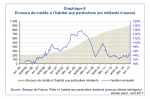
 l'encours en avril 2017 est de 900 milliards d'€.
l'encours en avril 2017 est de 900 milliards d'€.[lien réservé abonné]
✓ En 2017, les banques ont accordé chaque mois plus de 30 milliards d’euros de nouveaux crédits aux ménages.
[lien réservé abonné]
Autant pour moi, j'ai confondu évolution et montant de l'encours et lu sur la mauvaise échelle! (la courbe me surprenait un peu mais comme elle était communiquée par une personne au dessus de tout soupçon je l'ai prise pour argent comptantLatinGrec a dit:Trahison !l'encours en avril 2017 est de 900 milliards d'€.
 ).
).
Ce chiffre parait assez cohérent avec celui de 900 milliards en avril 2017.Aristide a dit:Suivant la Banque de France l’encours en crédits immobiliers était de 985 milliards d’euros à fin juillet 2018
Ce rythme me parait effréné. Si on considère une durée moyenne de 15 ans, l'encours serait de l'ordre de 15 x 30 X 12 = 5 400 milliards € après 15 ans! alors qu'il est de 985 milliards € en juillet 2018.En revanche, la Fédération Française des Banques (FBF) annonce 30 milliards de crédits nouveaux par mois en 2017 aux particuliers.
15 x 30 X 12 = 5 400 milliards €
A la réflexion quelque chose cloche en effet.Aristide a dit:Désolé mais prendre l'encours (en nombre ou en euros) pour base n'est pas adapté à votre recherche !
Cdt
 Votre PEL fermera en 2026 : où trouver un meilleur rendement sans risque ?
Votre PEL fermera en 2026 : où trouver un meilleur rendement sans risque ?
 Cette néobanque met la clé sous la porte, vous avez jusqu'au 11 novembre pour récupérer votre argent
Cette néobanque met la clé sous la porte, vous avez jusqu'au 11 novembre pour récupérer votre argent
 Le CAC 40 résiste au retour des taxes : le Journal de la Bourse du 26 septembre 2025
Le CAC 40 résiste au retour des taxes : le Journal de la Bourse du 26 septembre 2025
 Que deviennent les SCPI sans frais de BoursoBank désormais disponibles en assurance vie ?
Que deviennent les SCPI sans frais de BoursoBank désormais disponibles en assurance vie ?
 Assurance vie : ce que cachent les gros bonus de vos contrats
Assurance vie : ce que cachent les gros bonus de vos contrats
 Attention à cette arnaque au chèque, vous pouvez perdre gros
Attention à cette arnaque au chèque, vous pouvez perdre gros


