Aristide a dit:
Désolé, je n'ai pas la réponse.
J'ai pris les données fournies dans l'exemple et les ai actualisées comme il se doit.
Vous pouvez d'ailleurs vérifier que, partant des ces paramètres, la stricte application de l'équation ad hoc donne le même résultat que la fonction TRI (= Taux de Rendement Interne) de Excel.
NB) - Ce Taux de Rendement Interne (TRI) est en même temps le Taux de Rendement Annuel Actuariel Brut (T.R.A.A.B) puisque les flux de trésorerie sont supposés annuels.
Cdt
Je vais essayer de donner une explication, avec mes propres moyens et mon propre vocabulaire.
La question est:
Peut-on se baser sur le taux moyen des obligations d'un portefeuille pour déterminer le YTM (nota: pour moi, taux annualisé du portefeuille à un jour donné jusqu'à l'échéance)?
Je reprends l'exemple de @mattmatt01:
Une obligation de nominal 100€ au coupon de 6% réinvesti chaque année jusqu'à l'échéance de 6 ans, achetée à 110€, soit 10% au dessus de sa valeur de remboursement.
Intérêts acquis à l'échéance: 100 (1.06exp6-1) = 41,852€
Somme remboursée: 100 (nominal) + 41,852 (intérêts) = 141,85€
Taux global de rendement rapporté au prix d'achat de 110€: 141,852/110 = 1,2896 soit
28,96%
Taux annualisé: 100 (1,2896exp1/6-1) =
4,33%
Je retrouve bien le taux calculé par mattmatt01.
Ce qui signifie qu'à l'échéance des 6 ans je devrai récupérer 141,85€ (sous réserve des aléas de ce type de support (cf. p11849 @lebadeil).
Considérons maintenant un portefeuille constitué de 3 obligations:
-1 part au nominal de 100€ au taux de 4% réinvesti chaque année,
-1 part au nominal de 100€ au taux de 6% réinvesti chaque année,
-1 part au nominal de 100€ au taux de 8% réinvesti chaque année.
Le taux moyen pondéré de ce portefeuille vaut: (100x4+100x6+100x8)/300= 6, soit 6% comme dans l'exemple ci-dessus.
Il est acheté 330 €, 6 ans avant l'échéance de remboursement, soit avec une surévaluation de 10% comme ci-dessus.
Calculs des intérêts au bout de 6 ans:
-Obligation à 6 %: 41,852 € (selon calcul ci-dessus)
-Obligation à 4%: 26,532€ (je vous fais grâce des calculs qui sont les mêmes que ci-dessus)
-Obligation à 8%: 58,687€
Intérêts totaux: 127,07€
Somme remboursée à l'échéance: 300 (nominal) + 127,07 = 427,07€
Taux de rendement global rapporté au prix d'achat de 330€: 427,07/330 = 1,29415 soit
29,415%
Taux annualisé: 100 (1,29415exp1/6-1) = 1,04391 soit
4,39%
Conclusion: la réponse à la question posée est: "non".
Dans l'exemple simplifié étudié, la différence de taux n'affecte toutefois que la seconde décimale. Pour passer d'un YTM de 4,33% à plus de 5,00%, il faudrait a priori une très grande disparité dans la composition du portefeuille, difficile à imaginer.
L'explication doit se trouver ailleurs.
Nota: les éléments factuels donnés par @lebadeil ne sont pas contestables mais n'expliquent pas selon moi les écarts constatés par certains.
Il faudrait entrer dans et décortiquer les logiciels de calcul du YTM: on aurait peut-être des surprises! J'ai toujours pensé que ces logiciels devraient faire l'objet d'une certification par un organisme indépendant: est-ce le cas ?
Je reste preneur de toute observation..
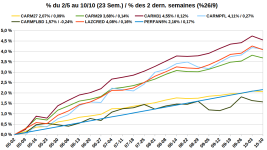
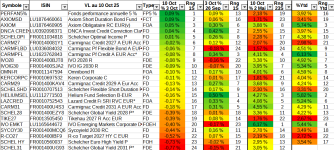
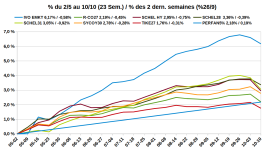
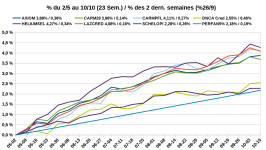
) mais j'ai quelques réticences à rentrer si haut. Les arguments en faveur d'une exposition à l'or restent cependant solides.
