Ageoff
Contributeur régulier
Aristide a dit:Cette hypothèse semble complètement utopique ???
Tu as pris 700 € au lieu de 600...
(mais cela ne change rien au caractère surnaturel de la demande)
Suivez la vidéo ci-dessous pour voir comment installer notre site en tant qu'application web sur votre écran d'accueil.
Note.: Cette fonctionnalité peut ne pas être disponible dans certains navigateurs.
Aristide a dit:Cette hypothèse semble complètement utopique ???

MacBidouille a dit:Il n'existe donc pas d'équation permettant de trouver le taux je suppose.
Exact.Ageoff a dit:Tu as pris 700 € au lieu de 600...
(mais cela ne change rien au caractère surnaturel de la demande)
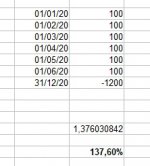
Normal car comme indiqué plusieurs fois dans les échanges antérieurs cette fonction calcule:Ageoff a dit:Il existe une formule, la fonction TRI.PAIEMENTS(valeurs; dates; [estimation]) citée plus haut, qui permet de calculer la rentabilité de placements non périodiques.
Ici, ça donne :
Afficher la pièce jointe 10252
(à noter une légère différence avec mon calcul manuel précédent)
Bonjour Aristide,Aristide a dit:
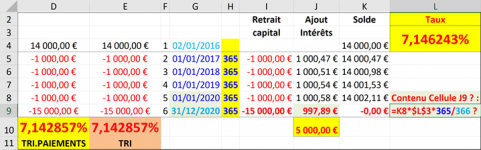
Bonjour, Non du tout;Marioux a dit:N’avez-vous pas essayé ou pu essayer votre simulation avec plus de Chiffres Significatifs, en prenant une Valeur plus proche de la réalité, par exemple : 7,14 286% ?
Bonjour moietmoi,moietmoi a dit:Bonjour, Non du tout;
je comprends que certains puissent s'intéresser au millième près, voire au dix millième;
Pour ma part, je m'en tiens au fait que le nombre de chiffres significatifs après la virgule n'a de sens que si la précision des autres données est de même proportion;
Tant mathématiquement que pratiquement, il est faux de faire tous ces calculs, avec autant de chiffres après la virgule , alors que l'on ne compte pas la variable de l'inflation pendant le temps du placement, et d'autres paramètres que je pourrais trouver, si j'y réfléchi, alors que cette simple inflation va plus jouer que le 2 ème chiffre significatif;(confusion entre stock et flux)
une loi d'expression des nombres, exprime que l'on ne doit pas indiquer les chiffres significatifs si ils sont supérieurs à la précision de l'instrument de mesure;
Ainsi avec un double décimètre gradué au mm, on estime que l'oeil peut distinguer le demi millimètre, il est donc faux de faire des calculs avec des chiffres de 7,14286 mètres;
Par ailleurs au niveau de la vraie vie, à quoi sert ce calcul , à part pour des comparaisons, dont les autres termes n'ont pas cette précision;
Je comprends cependant fort bien, la recherche qui est effectuée pour voir comment les logiciels collent à la réalité mathématique: je me souviens bien de ma première calculette ou je m'amusais à faire 10/3*3 et je ne retrouvais pas 10..... c'était dans le temps des premières calculettes....
Bien évidemment, il faut lire :Marioux a dit:Bonjour moietmoi,
14 000€ x 7,135% = 998,90€ (998,90€ / 14 000€ = 7,135% ~= 7,14…%)
Marioux a dit:Mais dois-je comprendre qu’il vous importe peu qu’un prêteur
oui complètement égal, si je comprends bien tu parles de 1 euro et quelques sur 5 ans? et tu voudrais que j'y fasse attention? que l'exercice intellectuel puisse avoir un intérêt, je le conçois, mais franchement à qui feras tu croire que cette somme a une importance pour ta vie?Marioux a dit:1 000,16€ (1 000,16€ + 14 000€ à la dernière échéance),
au lieu de 998,90€,
Bonjour moietmoi,moietmoi a dit:en justice , en référé tu auras raison, et sur le fond, tu auras tort, vu le préjudice non prouvé..... car quel juge pourrait croire que tu as un préjudice sur 5 ans de 1 euro......
Bonjour moietmoi,moietmoi a dit:Bonjour, Non du tout;
je comprends que certains puissent s'intéresser au millième près, voire au dix millième;
Pour ma part, je m'en tiens au fait que le nombre de chiffres significatifs après la virgule n'a de sens que si la précision des autres données est de même proportion;
Tant mathématiquement que pratiquement, il est faux de faire tous ces calculs, avec autant de chiffres après la virgule , alors que l'on ne compte pas la variable de l'inflation pendant le temps du placement, et d'autres paramètres que je pourrais trouver, si j'y réfléchi, alors que cette simple inflation va plus jouer que le 2 ème chiffre significatif;(confusion entre stock et flux)
une loi d'expression des nombres, exprime que l'on ne doit pas indiquer les chiffres significatifs si ils sont supérieurs à la précision de l'instrument de mesure;
Ainsi avec un double décimètre gradué au mm, on estime que l'oeil peut distinguer le demi millimètre, il est donc faux de faire des calculs avec des chiffres de 7,14286 mètres;
Par ailleurs au niveau de la vraie vie, à quoi sert ce calcul , à part pour des comparaisons, dont les autres termes n'ont pas cette précision;
Je comprends cependant fort bien, la recherche qui est effectuée pour voir comment les logiciels collent à la réalité mathématique: je me souviens bien de ma première calculette ou je m'amusais à faire 10/3*3 et je ne retrouvais pas 10..... c'était dans le temps des premières calculettes....
celui qui encombrerait la justice avec des telles choses, ne mériterait que d'être saisi sur ces biens propres au montant équivalent au temps passé par l'ensemble des intervenants;Marioux a dit:Trêve de plaisanterie !
Marioux a dit:Où est donc votre logique ?
la règle des arrondis n'est pas définie par moi;Marioux a dit:Et pourquoi, n’arrondissez-vous donc pas la fraction 1/14 à 7,1%, voire 7% ?
Non bien sûr ! Ni par moi, ni par aucun des contributeurs ici-bas, et sans doute heureusement d’ailleurs !moietmoi a dit:la règle des arrondis n'est pas définie par moi;
Bien entendu, il fallait lire 1 230€ au lieu de 1 240€ !Marioux a dit:Il me semble que l’on peut comprendre, ici, qu'une valeur calculée résultante d’un montant de 1 234,56 789€, par exemple, doit s’arrondir et s’afficher à au plus 2 décimales : 1 234,57€ ; 1 234,60€ ; 1 235€ ; 1 230€ ; 1 200€ ; voire 1 000€ selon que l’on en est, de manière contractuelle, à 1€C, 1€D, 1€, 10€, 100€ voire 1 000€ près
crois-tu vraiment que quelqu'un lise cela?Marioux a dit:Bien entendu, il fallait lire 1 230€ au lieu de 1 240€ !
Bonjour moietmoi,moietmoi a dit:crois-tu vraiment que quelqu'un lise cela?
J’avais cru comprendre que vous appliquiez les règles définies par les Textes Officiels :moietmoi a dit:Pour ma part, je m'en tiens au fait que le nombre de chiffres significatifs après la virgule n'a de sens que si la précision des autres données est de même proportion;
moietmoi a dit:c'est la légalité; on n'a pas le droit de faire autrement;
Non, c'est sans doute pourquoi vous m'avez dirigé vers le texte précité : Les arrondis [lien réservé abonné] et je vous en remercie !moietmoi a dit:la règle des arrondis n'est pas définie par moi;

 BNP Paribas, Société Générale : Crédit Agricole : la chute des banques s'amplifie sur le CAC 40
BNP Paribas, Société Générale : Crédit Agricole : la chute des banques s'amplifie sur le CAC 40
 Taxe foncière 2027 : une hausse ciblée de 63 euros en moyenne laissée au choix de votre futur maire
Taxe foncière 2027 : une hausse ciblée de 63 euros en moyenne laissée au choix de votre futur maire
 Impôt sur le revenu 2026 : la campagne de déclaration débutera le jeudi 9 avril
Impôt sur le revenu 2026 : la campagne de déclaration débutera le jeudi 9 avril
 Immobilier à Tours : stabilité des loyers et légère baisse des prix d'achat en mars 2026
Immobilier à Tours : stabilité des loyers et légère baisse des prix d'achat en mars 2026
 Paiement en plusieurs fois : faut-il s'inquiéter des nouvelles règles du crédit conso ?
Paiement en plusieurs fois : faut-il s'inquiéter des nouvelles règles du crédit conso ?
 Aspa : les nouveaux seuils 2026 pour rembourser à l'Etat le minimum vieillesse en cas de décès
Aspa : les nouveaux seuils 2026 pour rembourser à l'Etat le minimum vieillesse en cas de décès


