Calcul taux de rendement d'un placement avec retrait régulier

[moietmoi]

J'ai pensé à prendre en compte la moyenne des capitaux investis sur 5 ans mais je le sens pas : (14.000 + 13.000+12.000+11.000+10.000)/5 = 12.000 investi en moyenne. Prix de revente 15.000€. R= (15.000-12.000)/5 = 5%..

Pour parler de rendement, sans la fiscalité associé, il faudrait savoir le capital initial immobilisé
est ce que tu considères avoir immobilisé 15 000 euros ou pas;?

 

[MacBidouille]

Non j'ai immobilisé 14.000€ la 1ère année 13.000€ la 2ème, 12.000€ la 3ème, 11.000€ la 4ème et 10.000€ la 5ème

 

[moietmoi]

Non j'ai immobilisé 14.000€ la 1ère année 13.000€ la 2ème, 12.000€ la 3ème, 11.000€ la 4ème et 10.000€ la 5ème

tu peux donc faire un rendement par année;
peut être pourrais tu faire au global la rentabilité
20 000-15 000= 5000*100/20 000=25%
et le taux de rendement
20 000-15 000=5000*100/15 000=33,33%

mais je le répète, sans la fiscalité cela ne veut rien dire, surtout dans le montage considéré;

 

[Aristide]

Bonjour Aristide, et merci.. La crainte d'une erreur m'a assailli, un instant!!

 

[MacBidouille]

tu peux donc faire un rendement par année;
peut être pourrais tu faire au global la rentabilité
20 000-15 000= 5000*100/20 000=25%
et le taux de rendement
20 000-15 000=5000*100/15 000=33,33%

mais je le répète, sans la fiscalité cela ne veut rien dire, surtout dans le montage considéré;

Merci pour ton aide. La fiscalité n'a pas d'importance pour le moment, je cherche avant tout à définir un mode de calcul exact de rentabilité du capital investi. Je déduirai les charges une fois cela établi. Il me semble que ta proposition de calcul n'est pas bonne car elle ne tient pas compte des capitaux réellement engagés année après année. Je ne comprends pas non plus d'où viennent les 20.000€. Merci quand même.

 

[Aristide]

Avec ces nouvelles données, hors fiscalité, le taux de rendement est proche de 7,14%

Cdt

 

[moietmoi]

, je cherche avant tout à définir un mode de calcul exact de rentabilité du capital investi.

vu que comme tu les dis toi même il n'y a pas UN capital investi, mais plusieurs, ta question n'a pas de sens... à mon sens..... aucun sens; et mathématiquement parlant;

d'où viennent les 20.000€

la différence entre rendement et rentabilité; dans un cas on regarde l'investissement (ici au maximum 15 000) et dans l'autre on regarde ce qu'on en a retiré "intérêt" ou assimilé+ ce qu'est devenu le capital; toi tu as eu 5*1000+15 000; c'est la base de la différence entre la rentabilité et le rendement dans les entreprises, aussi en thermodynamique, en mécanique....
on peut très bien avoir une très forte rentabilité et un rendement médiocre et vice versa
exemple en immobilier un loyer très cher et la valeur du bien qui s'effondre... à l'inverse un loyer modéré mais une très forte plus value à la revente....

 

[MacBidouille]

Avec ces nouvelles données, hors fiscalité, le taux de rendement est proche de 7,14%

Cdt

Merci Aristide.

vu que comme tu les dis toi même il n'y a pas UN capital investi, mais plusieurs, ta question n'a pas de sens... à mon sens..... aucun sens; et mathématiquement parlant;


la différence entre rendement et rentabilité; dans un cas on regarde l'investissement (ici au maximum 15 000) et dans l'autre on regarde ce qu'on en a retiré "intérêt" ou assimilé+ ce qu'est devenu le capital; toi tu as eu 5*1000+15 000; c'est la base de la différence entre la rentabilité et le rendement dans les entreprises, aussi en thermodynamique, en mécanique....
on peut très bien avoir une très forte rentabilité et un rendement médiocre et vice versa
exemple en immobilier un loyer très cher et la valeur du bien qui s'effondre... à l'inverse un loyer modéré mais une très forte plus value à la revente....

Désolé si ma question n'a pas de sens pour toi, pour moi elle en bien puisque c'est comme ça que les choses se passent dans mon cas. En revanche ta réponse ne correspond toujours pas à mon cas puisque je n'ai pas eu 20.000 de capital comme je l'ai expliqué. J'ai mis 15.000€ de capital et j'ai récupéré 1000€de capital par an. C'est pas des intérêts non plus...c'est un désengagement des sommes investies avec malgré tout un bénéfice lors de la revente des parts restantes. Mais je convient que ce n'est pas courant et donc difficile à appréhender en terme de calcul.

 

[moietmoi]

Désolé si ma question n'a pas de sens pour toi, pour moi elle en bien puisque c'est comme ça que les choses se passent

non; tu cherches à définir un chiffre de rendement. il faut savoir à partir de quoi?

J'ai mis 15.000€ de capital et j'ai récupéré 1000€de capital par an

tu as mis 15 000 puis récupérer 5*1000 +15 000 à la fin; cela fait bien 20 000? ou alors je retourne en ce2......

malgré tout un bénéfice lors de la revente des parts restantes.

c'est la différence entre rendement et rentabilité;
pour la rentabilité on regarde exactement comme toi:à la fin combien est devenu ce qui reste....

 

[moietmoi]

je reviens sur ta question; pourait on la formuler ainsi:

a quel taux devrait être un livret sur lequel je verserais 15 000 euros en en retirant aussitôt 1000, puis 1000 chaque année pendant 4 ans au début de l'année, pour qu'à la fin de la 5 ème année il y ait 15 000 euros sur le livret?

à 8,9% on arrive à cela :15123 donc un peu au dessus.... il faut maintenant mettre en équation

15000-1000=14000
14000*8,9%= 1246 - 1000 retiré =246
14246*8,9%= 1267 -1000= 267
14246+267=14513 *8,9%=1292 -1000=292
14513+292=14805*8,9%=1318 -1000=318
14805+318=15123

 

[MacBidouille]

je reviens sur ta question; pourait on la formuler ainsi:

a quel taux devrait être un livret sur lequel je verserais 15 000 euros en en retirant aussitôt 1000, puis 1000 chaque année pendant 4 ans au début de l'année, pour qu'à la fin de la 5 ème année il y ait 15 000 euros sur le livret?

à 8,9% on arrive à cela :15123 donc un peu au dessus.... il faut maintenant mettre en équation

15000-1000=14000
14000*8,9%= 1246 - 1000 retiré =246
14246*8,9%= 1267 -1000= 267
14246+267=14513 *8,9%=1292 -1000=292
14513+292=14805*8,9%=1318 -1000=318
14805+318=15123

Oui la formulation est la bonne en effet. Je suppose que tu as trouvé le taux approximatif par le principe bien connu de tous les mathématiciens, c'est à dire l'équation dite du "Tâtonnement" ou encore du "pifomètre" , mais c'est bien ça. Pour ma part, et en suivant ton exemple j'ai trouvé 8.36%

	8.36%​
1​	14 000.00 €	1 170.40 €
2​	14 170.40 €	1 184.65 €
3​	14 355.05 €	1 200.08 €
4​	14 555.13 €	1 216.81 €
5​	14 771.94 €	1 234.93 €	15 006.87 €

Ce résultat est confirmé par la formule excel VC dans laquelle j'ai mis les versements périodiques en négatif afin qu'ils entrent en déduction du capital et non pas en augmentation =VC(I8.36%;5;-1000;14000;0) soit 15 006€.

Je pense que c'est la solution à mon problème. Merci pour ton aide moietmoi, ça me paraît plus clair maintenant.

 

[MacBidouille]

Avec ces nouvelles données, hors fiscalité, le taux de rendement est proche de 7,14%

Cdt

Merci Aristide pour ta suggestion. J'avais déjà tenté avec le TRI mais en avais déduit que ce n'était pas la bonne approche compte tenu de la particularité de mon problème. Je pense avoir trouvé la solution avec moietmoi qui a décortiqué le calcul que j'ai pu ensuite valider avec une fonction excel. Merci encore

 

[moietmoi]

c'est à dire l'équation dite du "Tâtonnement" ou encore du "pifomètre"

zut:!!! démasqué, pour moi qui suit favorable au port du masque....

 

[Ageoff]

Oui la formulation est la bonne en effet. Je suppose que tu as trouvé le taux approximatif par le principe bien connu de tous les mathématiciens, c'est à dire l'équation dite du "Tâtonnement" ou encore du "pifomètre" , mais c'est bien ça. Pour ma part, et en suivant ton exemple j'ai trouvé 8.36%

En l'occurrence, il faut mieux utiliser le principe bien connu des pros d'Excel, c'est-à-dire le solveur, qui permet d'obtenir exactement la valeur d'une cellule pour qu'une autre cellule calculée soit égale à une valeur donnée.

On trouve 8,35189...

	8.36%​
1​	14 000.00 €	1 170.40 €
2​	14 170.40 €	1 184.65 €
3​	14 355.05 €	1 200.08 €
4​	14 555.13 €	1 216.81 €
5​	14 771.94 €	1 234.93 €	15 006.87 €

Ce résultat est confirmé par la formule excel VC dans laquelle j'ai mis les versements périodiques en négatif afin qu'ils entrent en déduction du capital et non pas en augmentation =VC(I8.36%;5;-1000;14000;0) soit 15 006€.

Je pense que c'est la solution à mon problème.

Et c'est exactement comme ça qu'il faut faire.
Sauf que je ne comprends pas pourquoi tu as retiré 1000 une 5e fois.
À la fin de la dernière année, on ne retire pas 1000.

Tu arrives à 16000 en fin de cinquième année, alors qu'il faut arriver à 15000.



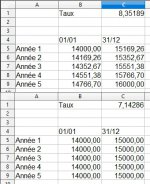
Et l'on trouve 7,14286... %

Qui n'est autre... mais oui... que le chiffre donné par Aristide !
(enfin, à un pouième près)

À noter que les chiffres obtenus avec ce taux semblent un peu bizarres, alors qu'il n'en est rien.
7,14 % est le taux qui permet d'avoir 1 k€ d'intérêts pour 14 k€.
Comme on retire 1 k€ chaque année, on repart de 14 k€ à chaque fois.
À la fin de la 5e année, hop, on reprend ses (14 + 1) k€.

Une question reste cependant sans réponse (du moins en ce qui me concerne).
Quel est l'intérêt d'investir 15 k€ et de retirer aussitôt 1 k€ ?

 

[Aristide]

Bonjour,

Normalement les intérêts sont capitalisés en fin d'année et l'année suivante des intérêts sont donc calculés sur la nouvelle valeur acquise avec intérêts capitalisés.

Avec la fonction "valeur cible/solveur" de Excel il n'en est pas ainsi puisque l'on recherche juste le taux qui donne 5.000€ d'intérêts au terme de la 5ème année.

Si l'on raisonne en appliquant ladite capitalisation les intérêts devraient donc être supérieurs à 5.000€.

Comme ce n'est pas le cas et que l'on reste avec 5.000€ d'intérêts au bout de 5 ans alors que la base annuelle des leur calcul est supposée accrues des intérêts capitalisés, il est logique que le taux de rentabilité qui en ressort ne soit plus que de 7,14%.

Cdt

 

[MacBidouille]

Bonjour à tous.
Merci pour votre aide précieuse. 7.14% est donc bien le bon résultat car j'avais en effet ajouter indûment 1000€ en fin de mon calcul la 5ème année.
Bonne journée

 

[jodel140]

Avec ces nouvelles données, hors fiscalité, le taux de rendement est proche de 7,14%

Cdt

Excel ... lent Aristide. Toujours un coup d'avance !

 

[Aristide]

 

[Anonyme]

En raisonnant en intérêts simples et en année civile (14000 empruntés, 4 annuités de 1000 et une 5° de 15000), on trouve le même résultat (7,142857143 %) :

taux	date	débit	crédit	jours	intérêts	capital	capital
annuel	(J/M/A)				courus	remboursé	restant dû
(en %)	01/01/2016	14000		0	0,00	0,00	14000,00
7,142857143	01/01/2017		1000	366	1000,00	0,00	14000,00
7,142857143	01/01/2018		1000	365	1000,00	0,00	14000,00
7,142857143	01/01/2019		1000	365	1000,00	0,00	14000,00
7,142857143	01/01/2020		1000	365	1000,00	0,00	14000,00
7,142857143	01/01/2021		15000	366	1000,00	14000,00	0,00

 

[Aristide]

Il semble que votre calcul ne soit pas réellement effectué en intérêts simples.

En effet, en appliquant le taux de 7,14...% au solde de 14.000€ l'on obtient bien 1.000€ d'intérêts.

Puis ces intérêts viennent d'abord s'ajouter au solde de 14.000€ pour le porter à 15.000€ ( = capitalisation) mais immédiatement réduit à nouveau à 14.000€ par le retrait de 1.000€ en capital.....et ainsi de suite.

Cdt