Calcul taux de rendement d'un placement avec retrait régulier

[Anonyme]

l'applicatif utilisé (pompé sur le bouquin Les calculs financiers du juriste) ne calcule les intérêts échus que sur le capital restant dû, et non sur le total dû (capital + intérêts échus impayés), donc sans aucune capitalisation, toujours vue avec méfiance par les juristes. Mais ça ne se voit pas car j'ai occulté les colonnes correspondantes et de toute façon dans le cas considéré il n'y a pas d'intérêts échus impayés.

Mais je ne comprends pas pourquoi TRI PAIEMENTS donne un résultat légèrement différent (7,134727 % avec les mêmes dates)

 

[Aristide]

l'applicatif utilisé (pompé sur le bouquin Les calculs financiers du juriste) ne calcule les intérêts échus que sur le capital restant dû, et non sur le total dû (capital + intérêts échus impayés), donc sans aucune capitalisation, toujours vue avec méfiance par les juristes. Mais ça ne se voit pas car j'ai occulté les colonnes correspondantes et de toute façon dans le cas considéré il n'y a pas d'intérêts échus impayés.

Oui mais nous sommes bien d'accord que,contrairement au calcul par "Valeur cible/solveur" qui donne un taux de 8,33% la différence vient que dans ce calcul les intérêts (= 5.000€ d'intérêts au terme des 5 ans) sont "calculés" sans tenir compte de quelque capitalisation que ce soit contrairement à votre calcul et au mien.

Mais je ne comprends pas pourquoi TRI PAIEMENTS donne un résultat légèrement différent (7,134727 % avec les mêmes dates)

Excel propose deux fonctions:

=> La fonction "TRI" qui calcule un taux proportionnel.
Cette fonction raisonne en périodes - qui doivent être régulières - et ne tient donc aucun compte des dates.
Dans le cas traité cette fonction aurait calculé un taux proportionnel en considérant 5 années pleines même si, en réalité, il manque un jour la dernière année (donc périodicité pas tout à fait régulière).

=> La fonction "TRI.PAIEMENTS" qui calcule un taux actuariel
Cette fonction tient compte des dates exactes des flux de trésorerie.
Elle calcule en jours sauf qu'elle ignore les années bissextiles (= toujours 365 jours).

Quand il s'agit de flux annuels de trésorerie, le taux proportionnel (=TRI) est normalement identique au taux actuariel (= TRI.Paiements) et inversement.

Peut-être que la légère différence que vous relatez provient de ce calcul "jour et 365j/an" ?

Cdt

 

[moietmoi]

Bonjour,
j'en reviens à mes premiers commentaires sur le sens de la question; et la définition des paramètres;
Si on s'intéresse au rendement ou à la rentabilité, c'est entre autre pour pouvoir faire des comparaisons avec d'autres produits ou montages financiers;
Le résultat (sauf erreur) est toujours mathématiquement juste, mais souvent faux par rapport à la réalité,car on ne prend pas soin de décrire la réalité dans les équations mathématiques
Dans la réalité il existe peu( ou pas) de placement à capitalisation au jour le jour,c'est souvent annuel, et souvent lorsqu'un retrait est effectué, c'est la quinzaine , en terme d'intérêt qui est annulé;

Par ailleurs sur les placements à plus value, on évalue le rendement annuel sur la base d'une plus value annuelle; et les taux indiqués par la presse et moneyvox sont des taux d'un équivalent à capitalisation annuelle;
C'est ainsi pour les taux annoncés sur constat d'assurance vie à postériori, chaque année en parlant des taux de rendement de l'année n-1;
Comme nous ne sommes pas sur un forum mathématique, il nous faudrait sans doute définir pour le calcul simulé d'un livret répondant à la demande de Macbidoulle, une capitalisation annuelle avec comptabilsation du retrait annulant la quainzaine en intérêts afférant à cette quinzaine;

 

[Aristide]

et souvent lorsqu'un retrait est effectué, c'est la quinzaine , en terme d'intérêt qui est annulé;

Ceci n'est vrai que pour les livret et, dans quelques banques, pour les PEL

Dans la réalité il existe peu( ou pas) de placement à capitalisation au jour le jour,c'est souvent annuel,

Par ailleurs sur les placements à plus value, on évalue le rendement annuel sur la base d'une plus value annuelle; et les taux indiqués par la presse et moneyvox sont des taux d'un équivalent à capitalisation annuelle;
C'est ainsi pour les taux annoncés sur constat d'assurance vie à postériori, chaque année en parlant des taux de rendement de l'année n-1;

Ainsi qu'expliqué ci-dessus, sur une année pleine la périodicité de capitalisation importe peu et le taux proportionnel est le même que le taux actuariel.

Prenons un exemple, pour cas d'école, avec un placement AV de 10.000€ à 1%.

=> Au bout d'un an la valeur acquise sera de 10.000€ x 1,01 = 10.100€

=> Si la capitalisation est journalière le taux journalier sera :
+ 1,01= (1+Ij)^(365)
+ Ij = ((1,01^(1/365) - 1)
+ Au 31 janvier la valeur acquise sera de 10.000€ x (1,01^(31/365)) = 10.008,45€
+ Au 30 juin la valeur acquise sera de 10.000€ x (1,01^(181/365)) = 10.049,46€
+ Au 31 décembre la valeur acquise sera de 10.000€ x (1,01^(365/365)) = 10100€

S'il y a des versements ou des retraits, quelles que soient leurs dates, les nouvelles valeurs acquises en cours d'années sont calculées, sur les nouveaux soldes, suivant le même principe.

Cdt

 

[Marioux]

Bonjour à tous.
Merci pour votre aide précieuse. 7.14% est donc bien le bon résultat car j'avais en effet ajouter indûment 1000€ en fin de mon calcul la 5ème année.
Bonne journée

Bonjour MacBidouille,
Le Taux Fixe Annuel qui permet de rapporter 1 000€ par An à partir d'un Capital Initial de 14 000€ se calcule aisément : Taux = 1 000€ / 14 000€ = 1 / 14 = 0,07 142 85... = 7,142 857…% ! : À chaque fois les 6 Chiffres Soulignés constituent une Période (Au sens Mathématique du terme) et se répètent à l'infini ! ...
Après ça, on peut Afficher ce Taux avec le Nombre choisi de Chiffres Significatifs nécessaires :
7% ; 7,1% ; 7,14% ; 7,143% ; 7,142 9% ; 7,142 86% ; 7,142 857% ...
Cdt

 

[moietmoi]

En simulant sur moneyvox en assurance vie
Capital initial 14000 capital atteint 14000 rachat fin d'année 1000 euros.7,14%
Année Intérêts annuels Solde Nombre de rachats Montant total des rachats Dont intérêts imposables
2021 999,60 € 13.999,60 € 1 1.000,00 € 66,64 €
2022 999,57 € 13.999,17 € 1 1.000,00 € 128,84 €
2023 999,54 € 13.998,71 € 1 1.000,00 € 186,90 €
2024 999,51 € 13.998,22 € 1 1.000,00 € 241,08 €
2025 999,47 € 13.997,69 € 1 1.000,00 € 291,66 €
Total 4.997,69 € 13.997,69 € 5 5.000,00 €
Le retrait de fin d'année cumulé au capital 15000.à
Epsilon près..

 

[MacBidouille]

Encore une fois, merci à tous de votre participation.
Je me pose maintenant la question du calcul du taux de rentabilité, hors fiscalité, de cette opération.

J'ai donc acheté pour 14.000€ de parts sociales la 1ère année au 1er janvier et sans aucun intérêt perçu.
La seconde année j'ai vendu pour 1.000€ de parts sociales, idem la 3ème-4ème et 5ème année et à chaque fois au 1er janvier. Je précise que j'ai vendu les parts au prix d'achat.
Au 31 décembre de la 5ème année j'ai vendu les parts sociales qui me restaient pour 15.000€

Dans mon idée, je me dis que je dois calculer la moyenne des sommes investies sur les 5 ans soit 12.000€ :
(14.000+13.000+12.000+11.000+10.000)/5 = 12.000

et ensuite diviser le bénéfice (15.000-12.000) = 3.000€ par le montant moyen investi 12.000€
soit une rentabilité de 25% ramené à l'année à 5% brut de fiscalité (je précise pour moietmoi)

Quelque chose me dit que ç'est pas aussi simple que ça ?

 

[Aristide]

Bonjour,

Ce calcul est inexact; la réponse vous a été fournie ci-dessus par divers intervenants.

Cdt

 

[Aristide]

Bonsoir,

Mais je ne comprends pas pourquoi TRI PAIEMENTS donne un résultat légèrement différent (7,134727 % avec les mêmes dates)

J'ai la réponse à votre interrogation.

Explications dans le nouveau fichier Excel joint.

Remarquions d'abord que la fonction "TRI" de EXCEL qui ne permet que des calculs en taux proportionnels sur des échéances régulières donne un résultat de 7,142857%.

Dans l'absolu ce taux de rentabilité proportionnel n'est pas exact puisqu'il manque un jour à la dernière année pour que le condition de "périodicités régulières" soit respectée.

Ensuite la fonction TRI.PAIEMENT. donne un taux actuariel de 7,138232% et ce résultat est confirmé par le développement de l'équation d'actualisation (matérialisation en rose saumon).

Puis, enfin, le calcul que vous relatez "Les calculs financiers du juriste" du juge Biardeaud sur lequel nous avions déjà échangé, donne un taux de 7,134727% et je le retrouve bien dans l'équation d'actualisation développée sur la droite (matérialisation en jaune)

L'explication vient d'une manière différente de comptage des jours.

EXCEL compte les jours par différences entre les dates des flux de trésorerie considérés.

En revanche "Les calculs financiers du juriste" les compte par rapport aux mêmes dates de l'année précédente.

Ainsi l'on voit que dans la premier cas la période porte sur 1826 jours alors que dans le second cas elle porte sur 1827 jours

Dans les deux cas l'année n'est comprise que pour 365 jours.

Les deux calculs sont actuariels et, concernant "Les calculs financiers du juriste" le décompte des jours par rapport a "A-1" laisse penser que c'est l'applicatif de calcul du TAEG que vous avez utilisé.

En effet cette façon de faire a été indiquée dans le décret du mai 2016 concernant le TAEG avec cet ajout "ainsi que le taux débiteur".

Mais, ce qui est curieux, c'est que, dans l'autre file sur le calcul Lombard, sur ma demande, Mr Lasserre Capdeville a interrogé le juge Biardeau sur ledit ajout.

Ce dernier a répondu qu'il s'agissait d'un "cavalier juridique" et que si la méthode était bien applicable au TAEG, selon lui, elle ne l'était pas au taux débiteur.

Je crois d'ailleurs me souvenir que vous partagiez cet avis.

Toujours est-il que un jour de différence explique bien la différence de résultat que vous soulignez.

Cdt

 

[Anonyme]

Bonsoir,

J'ai la réponse à votre interrogation.

Explications dans le nouveau fichier Excel joint.

Remarquions d'abord que la fonction "TRI" de EXCEL qui ne permet que des calculs en taux proportionnels sur des échéances régulières donne un résultat de 7,142857%.

Dans l'absolu ce taux de rentabilité proportionnel n'est pas exact puisqu'il manque un jour à la dernière année pour que le condition de "périodicités régulières" soit respectée.

Ensuite la fonction TRI.PAIEMENT. donne un taux actuariel de 7,138232% et ce résultat est confirmé par le développement de l'équation d'actualisation (matérialisation en rose saumon).

Puis, enfin, le calcul que vous relatez "Les calculs financiers du juriste" du juge Biardeaud sur lequel nous avions déjà échangé, donne un taux de 7,134727% et je le retrouve bien dans l'équation d'actualisation développée sur la droite (matérialisation en jaune)

L'explication vient d'une manière différente de comptage des jours.

EXCEL compte les jours par différences entre les dates des flux de trésorerie considérés.

En revanche "Les calculs financiers du juriste" les compte par rapport aux mêmes dates de l'année précédente.

Ainsi l'on voit que dans la premier cas la période porte sur 1826 jours alors que dans le second cas elle porte sur 1827 jours

Dans les deux cas l'année n'est comprise que pour 365 jours.

Les deux calculs sont actuariels et, concernant "Les calculs financiers du juriste" le décompte des jours par rapport a "A-1" laisse penser que c'est l'applicatif de calcul du TAEG que vous avez utilisé.

En effet cette façon de faire a été indiquée dans le décret du mai 2016 concernant le TAEG avec cet ajout "ainsi que le taux débiteur".

Mais, ce qui est curieux, c'est que, dans l'autre file sur le calcul Lombard, sur ma demande, Mr Lasserre Capdeville a interrogé le juge Biardeau sur ledit ajout.

Ce dernier a répondu qu'il s'agissait d'un "cavalier juridique" et que si la méthode était bien applicable au TAEG, selon lui, elle ne l'était pas au taux débiteur.

Je crois d'ailleurs me souvenir que vous partagiez cet avis.

Toujours est-il que un jour de différence explique bien la différence de résultat que vous soulignez.

Cdt

Merci pour ces explications, le fichier est clair (même si je n'ai pas bien compris la colonne O) ; la différence est donc principalement liée au mode de calcul de TRI PAIEMENTS, qui actualise (dans notre exemple) chaque mouvement à l'aide d'une fraction dont le numérateur est 365 ou 366, tandis que le dénominateur est toujours 365.

 

[Aristide]

Bonjour,

La colonne "O" est l'équivalent de la colonne "G" mais avec comptage des jours par différence avec la même date un an avant (décret mai 2016) => D'où un total avec jour de plus.

Cdt

 

[Marioux]

En simulant sur moneyvox en assurance vie
Capital initial 14000 capital atteint 14000 rachat fin d'année 1000 euros.7,14%
Année Intérêts annuels Solde Nombre de rachats Montant total des rachats Dont intérêts imposables
2021 999,60 € 13.999,60 € 1 1.000,00 € 66,64 €
2022 999,57 € 13.999,17 € 1 1.000,00 € 128,84 €
2023 999,54 € 13.998,71 € 1 1.000,00 € 186,90 €
2024 999,51 € 13.998,22 € 1 1.000,00 € 241,08 €
2025 999,47 € 13.997,69 € 1 1.000,00 € 291,66 €
Total 4.997,69 € 13.997,69 € 5 5.000,00 €
Le retrait de fin d'année cumulé au capital 15000.à
Epsilon près..

Bonjour moietmoi,
Sachant que le Taux Fixe Annuel rapportant 1 000€/An pour un Capital Initial de 14 000€ est de :
1/14, soit 7,142 857…% (Seule Valeur donnant le bon Résultat sans nécessité d'Arrondir :
14 000€ x 1/14 = 1 000€ !), un Taux Fixe Annuel de 7,14% ne rapporte que :
14 000€ x 7,14% = 999,60€ < 1 000€, ce qui explique votre "Epsilon" ! :
N’avez-vous pas essayé ou pu essayer votre simulation avec plus de Chiffres Significatifs, en prenant une Valeur plus proche de la réalité, par exemple : 7,14 286% ?
Cdt.

 

[Aristide]

Bonjour,

Le retrait de fin d'année cumulé au capital 15000.à
Epsilon près..

Quelque chose me dit que ç'est pas aussi simple que ça ?

Je suis désolé mais je répète que, dans l'absolu, aucun des calculs ci-dessus n'est parfaitement exact.

D'abord le calcul 1.000/14.000 qui donne un taux de 7,142857...% ne serait vrai que sur les quatre premières années.

En effet la dernière année le retrait soldant a été effectué :
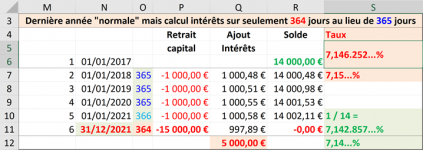
+ Au 364 ème jour (et non pas 365J) si l'on se situe dans une année normale
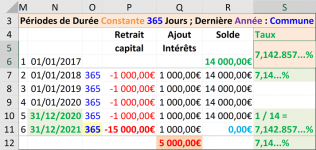
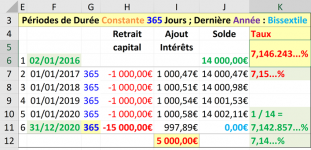
+ Au 365 ème jour (et non pas 366J) si l'on se situe dans une année bissextile.

Ainsi si l'on conservait ce taux:

+ Pour l'année normale les intérêts sur une année pleine seraient de 14.000€ x (1.000/14.000) / 364 x 365 = 1.002,75€ et non plus 1.000€.
Pour obtenir 1.000€ en 364 jours il faudrait appliquer une taux de :
T = 1.000 / ( 14.000/100/365 x 364) = 7,162480...%
=> 14.000€ x 7,162480...% / 365 x 364 = 1.000€

+ Pour l'année bissextile les intérêts sur une année pleine seraient de 14.000€ x (1.000/14.000) / 365 x 366 = 1.002,74€ et non plus 1.000€.
Pour obtenir 1.000€ en 365 jours il faudrait appliquer une taux de :
T = 1.000 / ( 14.000/100/366 x 365) = 7,162426...%
=> 14.000€ x 7,162426...% / 366 x 365 = 1.000€.

Dès lors, sur toute la période de 4 ans et 364 jours ou 4 ans et 365 jours il est impossible que le taux d'ensemble soit de 7,142857...% ainsi que calculé sur les quatre premières années pleines.

La remarque vaut exactement de la même façon et pour la même raison pour le résultat donné par la fonction "TRI" de EXCEL ainsi que je l'ai déjà précisé plusieurs fois.

En ce qui concerne la fonction "TRI.PAIEMENTS" de ce même EXCEL le résultat n'est pas non plus satisfaisant du fait:
+ D'un calcul en jours
+ D'une année civile toujours prise pour 365 jours (= années bissextiles ignorées)
+ D'un calcul actuariel
=> Il faut rappeler qu'avec un tel calcul:
+ Le taux résultant est supérieur au taux proportionnel si la périodicité de capitalisation est inférieure à l'année
+ Le taux résultant est égal au taux proportionnel si la périodicité de capitalisation est égale à l'année
+ Le taux résultant est inférieur au taux proportionnel si la périodicité de capitalisation est supérieure à l'année
Lorsque la période comprend des années bissextiles (numérateur) alors qu'au dénominateur Excel ne retient que 365 jours l'on se situe dans ce cas de figure.

C'est la même explication avec l'applicatif "Les calculs financiers du juriste" utilisé par casaminor avec, en plus, un comptage de jours par rapport à "A-1" qui a été imposé par un décret de mai 2016....mais qui concerne le calcul du TAEG.

A noter que j'avais bien pris la précaution de préciser:

Avec ces nouvelles données, hors fiscalité, le taux de rendement est proche de 7,14%

Par ailleurs MacBidouille nous a indiqué qu'il avait retiré 1.000€ de capital les quatre premières années et 15.000€ la dernière année laissant - à ce terme ( 4 ans + 364 j ou 4 ans + 365j)- un total d'intérêts de 5.000€.

Il n'a jamais dit qu'il avait perçu 1.000€ chacune des années considérées.

De fait, dans le nouveau tableau Excel joint, vous pourrez constater:
+ Qu'il n'en est pas ainsi
+ Que le taux exact sur 4 ans + 364 jours (année = 365 j) est de 7,146252...%
+ Que le taux exact sur 4 ans + 365 jours (année = 366 j) est de 7,146243...%.

A toutes fins utiles.

Cdt

 

[Marioux]

De fait, dans le nouveau tableau Excel joint, vous pourrez constater:
+ Qu'il n'en est pas ainsi
+ Que le taux exact sur 4 ans + 364 jours (année = 365 j) est de 7,146252...%
+ Que le taux exact sur 4 ans + 365 jours (année = 366 j) est de 7,146243...%.

Bonjour Aristide,
Deux valeurs, ici, différentes, mais quelle que soit la dernière année, bissextile ou non, le résultat arrondi est de :
7,146…%, voire 7,15…% #> 7,14…%, Taux jusqu’alors annoncé, par exemple aux Posts #35, 40 et 49 :

Comme ce n'est pas le cas et que l'on reste avec 5.000€ d'intérêts au bout de 5 ans alors que la base annuelle des leur calcul est supposée accrues des intérêts capitalisés, il est logique que le taux de rentabilité qui en ressort ne soit plus que de 7,14%.

En effet, en appliquant le taux de 7,14...% au solde de 14.000€ l'on obtient bien 1.000€ d'intérêts.
Puis ces intérêts viennent d'abord s'ajouter au solde de 14.000€ pour le porter à 15.000€ ( = capitalisation) mais immédiatement réduit à nouveau à 14.000€ par le retrait de 1.000€ en capital.....et ainsi de suite.

Remarquions d'abord que la fonction "TRI" de EXCEL qui ne permet que des calculs en taux proportionnels sur des échéances régulières donne un résultat de 7,142857%.
Dans l'absolu ce taux de rentabilité proportionnel n'est pas exact puisqu'il manque un jour à la dernière année pour que le condition de "périodicités régulières" soit respectée.

Je suis bien d’accord pour peu que la valeur, plus précise, du Taux soit celle de :
1 / 14 = 7,142 857…% (@ 7,14…%) que j’ai personnellement évoquée.
En effet, ici, il faut noter que, par exemple :
(7,1382% x 14 000€ = 999,35€) < (7,14% x 14 000€ = 999,60€) < 1 000€ !
Naturellement, je vous rejoins sur le point particulier suivant : Avec un terme un jour plus tôt (31/12/2021 au lieu de 01/01/2022), le Taux Annuel (Disons plutôt Annualisé !) Effectif Global (TAEG) est impacté et supérieur à 1/14 puisque la dernière échéance est de durée inférieure à celle d’une année complète ! :

Toutes les dates ont leur importance, et non pas uniquement la dernière !
Imaginez que le seul jour manquant se situe l’année précédente (31/12/2020 au lieu de 01/01/2021) ;
La dernière année étant encore commune, on obtient :

On se retrouve alors avec 5 périodes de durée constante (365 Jours), donc des échéances régulières pour lesquelles la fonction TRI d’EXCEL donne bien un Taux exactement égal à 1/14 ! ; Et, surtout, le TAEG est cette fois bien égal à cette valeur ! : Tout semble au mieux dans le meilleur des mondes ! ...
Mais si l’on considère un cas, toujours de 5 périodes de 365 Jours, avec la dernière année bissextile, on obtient :

La fonction TRI d’EXCEL donne toujours un Taux exactement égal à 1/14 alors que le TAEG est cette fois d’une valeur différente ! : Est-ce bien logique et sinon où se situe donc le problème, à votre avis ?
Cdt.

 

[MacBidouille]

Bonjour à tous.
Mon problème de calcul de rentabilité est donc maintenant réglé avec la fonction TRI d'excel et je vous en remercie. Je me permet de vous exposer une autre équation à résoudre pour finaliser totalement mon étude.
- Je fais pendant 6 mois des versements de 100€ sur un placement capitalisé (intérêts calculés tous les mois).
- Au bout de 6 mois je stoppe les versements et laisse l'argent sur le compte.
- Au bout de 12 mois je récupère 1200€ qui représentent le capital et les intérêts.
Quelle est l'équation qui me permet de déterminer le Taux de ce placement ?
Si nécessaire, on peut considérer que les versements des 6 premiers mois ont été placés à 5% l'an.
Merci d'avance pour votre aide.

 

[Aristide]

Bonjour,

Mon problème de calcul de rentabilité est donc maintenant réglé avec la fonction TRI d'excel et je vous en remercie. Je me permet de vous exposer une autre équation à résoudre pour finaliser totalement mon étude.

Si le résultat donné par la fonction "TRI" vous satisfait; très bien.
Mais je répète que - dans l'absolu - il n'est pas parfaitement exact puisque cette fonction n'admet que des périodicités régulières.
Or, dans votre cas, suivant les données que vous avez fournies il manque un jour à la dernière année pour avoir une année pleine.

- Je fais pendant 6 mois des versements de 100€ sur un placement capitalisé (intérêts calculés tous les mois).

"Calculé" ne veut pas forcément dire "capitalisé"
Ces intérêts sont "calculés" tous les mois mais est-ce qu'ils sont aussi capitalisés tous les mois ?
Ou bien les intérêts calculés chaque fin de mois ne sont-ils capitalisés qu'au terme des 6 mois ?

Cdt

 

[MacBidouille]

Il sont capitalisés tous les mois.

 

[Aristide]

La fonction TRI d’EXCEL donne toujours un Taux exactement égal à 1/14 alors que le TAEG est cette fois d’une valeur différente ! : Est-ce bien logique et sinon où se situe donc le problème, à votre avis ?

????

 

[Aristide]

Il sont capitalisés tous les mois.

Cette hypothèse semble complètement utopique ???
Cdt

 

[Ageoff]

- Je fais pendant 6 mois des versements de 100€ sur un placement capitalisé (intérêts calculés tous les mois).
- Au bout de 6 mois je stoppe les versements et laisse l'argent sur le compte.
- Au bout de 12 mois je récupère 1200€ qui représentent le capital et les intérêts.
Quelle est l'équation qui me permet de déterminer le Taux de ce placement ?

Euh... Tu es sûr de ton coup ?
Si tu plaçais les 600 € le 1er janvier, pour sortir à 1200 €, il faudrait déjà un taux annuel de 100 %.
Comme tu répartis les versement sur 6 mois, le taux sera évidemment supérieur.
Et concrètement, on trouve un taux mensuel de 7,48 % pour un taux annuel de 137,73 %...