Aristide
Top contributeur
Bonjour,

Peut-être est-ce la période de congés qui est l'explication de leur absence ?
Un décret qui me donne tort ?
Par exemple le dernier en date N° 2016-884 du 29 juin 2016 repris dans l'article R.314-3 du code de la consommation qui précise:
=> me donnent- t-il tort ?
N'y est-il pas écrit en français parfaitement correct et - sauf à être de mauvaise foi - parfaitement compréhensible :
=> La durée de la période doit être expressément communiquée à l'emprunteur ?
=> L'équation de base, qui définit le taux annuel effectif global (TAEG), exprime sur base annuelle ?
En pièce jointe vous trouverez le quatrième exemple traité à l'annexe des décrets N° 2002-927 et 928 du 11 juin 2002 et 2011-135 du 1er février 2011.
Je retrouve très exactement le TAEG affiché ou JO = 13,19%
Expliquez nous donc où vous trouvez la trace et donc l'utilité d'un taux périodique pour obtenir le TAEG recherché ?
Qui est de bonne foi et qui ne l'est pas ?
Oh oui; c'est extrêmement pontifiant via un "copier/coller" de reproduire in extenso un extrait du code de la consommation et de lire, tout simplement, ce qui y est écrit !!!
Contrairement aux intentions et qualifications que l'on m'attribue, si les uns et/ou les autres des vrais professionnels, juristes et/ou experts financiers ci-dessus évoqués, m'expliquent - bien entendu avec des arguments probants - que je suis dans l'erreur, c'est bien volontiers - après analyse/réflexion de ladite argumentation - que, le cas échéant je le reconnaitrais.
Cdt
Vous avez parfaitement raison; bis répétitaMembre39498 a dit:Je n'irai pas plus loin

Oui mais à ce propos il me semblerait intéressant que les intervenants professionnels - juristes et/ou experts financiers - vrais sachants, donnent leur interprétation des ces textes.car les lecteurs du forum ont maintenant suffisamment d'éléments pour se faire leur propre opinion.
Peut-être est-ce la période de congés qui est l'explication de leur absence ?
????Le fait d'écarter d'un revers de manche un décret qui vous donne tort
Un décret qui me donne tort ?
Par exemple le dernier en date N° 2016-884 du 29 juin 2016 repris dans l'article R.314-3 du code de la consommation qui précise:
Article R314-3
"Pour toutes les opérations de crédit autres que celles mentionnées à l'article R. 314-2, le taux annuel effectif global mentionné à l'article L. 314-3 est calculé à terme échu, exprimé pour cent unités monétaires, selon la méthode d'équivalence définie par la formule figurant en annexe au présent code.
La durée de la période doit être expressément communiquée à l'emprunteur.
……….."
=> L’annexe évoquée
ANNEXE mentionnée à l'article R.314-3
PARTIE I : Équation de base traduisant l'équivalence des prêts, d'une part, et des remboursements et charges, d'autre part.
L'équation de base, qui définit le taux annuel effectif global (TAEG), exprime sur base annuelle l'égalité entre, d'une part, la somme des valeurs actualisées des utilisations du crédit et, d'autre part, la somme des valeurs actualisées des montants des remboursements et paiements des frais, soit:
=> et « la formule figurant en annexe » :
SIGMA k=1 à m Ck (1+X)^-tk = SIGMA l =1 à m' Dl(1+X)^-SI
Avec, dans la signification des symboles, « X est le TAEG »
[lien réservé abonné]
=> me donnent- t-il tort ?
N'y est-il pas écrit en français parfaitement correct et - sauf à être de mauvaise foi - parfaitement compréhensible :
=> La durée de la période doit être expressément communiquée à l'emprunteur ?
=> L'équation de base, qui définit le taux annuel effectif global (TAEG), exprime sur base annuelle ?
En pièce jointe vous trouverez le quatrième exemple traité à l'annexe des décrets N° 2002-927 et 928 du 11 juin 2002 et 2011-135 du 1er février 2011.
Je retrouve très exactement le TAEG affiché ou JO = 13,19%
Expliquez nous donc où vous trouvez la trace et donc l'utilité d'un taux périodique pour obtenir le TAEG recherché ?
Qui n'est pas sérieux ?me semble peu sérieux,
Qui est de bonne foi et qui ne l'est pas ?
mais je vous laisse à vos certitudes pontifiantes.
Oh oui; c'est extrêmement pontifiant via un "copier/coller" de reproduire in extenso un extrait du code de la consommation et de lire, tout simplement, ce qui y est écrit !!!
Contrairement aux intentions et qualifications que l'on m'attribue, si les uns et/ou les autres des vrais professionnels, juristes et/ou experts financiers ci-dessus évoqués, m'expliquent - bien entendu avec des arguments probants - que je suis dans l'erreur, c'est bien volontiers - après analyse/réflexion de ladite argumentation - que, le cas échéant je le reconnaitrais.
Cdt
Pièces jointes
-
La consultation des
pièces jointes est
réservée aux abonnés
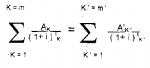




 )!)
)!)