Aristide
Top contributeur
Pfff !!!
Apprenez la logique de fonctionnement d'Excel !
Apprenez la logique de fonctionnement d'Excel !
Pièces jointes
-
La consultation des
pièces jointes est
réservée aux abonnés
Suivez la vidéo ci-dessous pour voir comment installer notre site en tant qu'application web sur votre écran d'accueil.
Note.: Cette fonctionnalité peut ne pas être disponible dans certains navigateurs.
En l'occurrence, il ne s'agit pas de la logique d'Excel qui ne fait qu'exécuter ce que vous lui demandez, mais de votre propre Logique qui me semble, ici, quelque peu défaillante puisque vous insistez tant :Aristide a dit:Pfff !!!
Apprenez la logique de fonctionnement d'Excel !
Je suis bien d'accord avec cela !Il faudrait être logique et cohérent dans tout le processus de calcul.
Là, je le suis beaucoup moins !Les échéances ont été calculées sur trois mois soit 1/4 d'année.
Non, 3,65 % / 12 = 0,30 416…% est le bien le Taux Mensuel !Et puisque l'échéance est supposée mensuelle le taux périodique "mensuel" qui a servi au calcul des échéances est donc de 3,65/1200 = 0,003416666....
Bien sûr que si !Et vous voudriez que le coefficient "Rapport entre la durée de l'année civile et celle de la période unitaire soit de 365/30 = 12,1666666...... ???
Eh bien non !
Non ! : La Durée du Prêt n’est effectivement pas de 3 Mois, mais de 3P x 30J = 90 Jours Global !S'il en est ainsi la durée du prêt n'est pas de 3 mois mais de 365/30/4 = 3,0446666666.....mois.
Oui, le Taux de Période (Périodique !) est de 3,65% / 365J x 30J = 0,3% !Et le taux de période de 3,65/100/(365/30) = 0,003.
? ? ?Mais en pratiquant ainsi, compte tenu des intérêts calculés sur 30 jours la 3è échéance est beaucoup plus élevée que les deux premières (~/~ 138€).
Le Taux Débiteur (Proportionnel ou Actuariel) peut être Égal au Taux de l’Intérêt Conventionnel (Proportionnel ou Annuel) Fixé au Contrat, mais il peut en Diverger ne serait-ce que par l’application des Arrondis Nécessaires ou de la Méthode de Calcul employée pour déterminer=> Tous s'accordent pour dire que le taux débiteur = le taux nominal proportionnel = le taux contractuel.
Je suis d'accord avec vous ! : C’est, ici, un Calcul Inversé !=> Ce Taux de l'Intérêt Conventionnel Proportionnel Annuel sert à calculer les intérêts compris dans les échéances et - éventuellement - l'échéance constante ce qui n'est nullement une obligation (Possibilité d'échéances progressives/dégressives/mixtes - régulières ou apériodiques - calculées ou non si directement choisies à priori = imposées par l'emprunteur et/ou le prêteur).
=> Le TRI peut tout à fait être calculé sans connaitre le Tauxdébiteurde l'Intérêt Conventionnel Proportionnel Annuel ni les intérêts compris dans les échéances puisque sa base de calcul est les échéances.
Pas du tout ! : C’est un Cas d’École qui permet de voir l'Incidence des Arrondis et justifie que, sans eux, le Taux Débiteur Proportionnel Calculé a effectivement bien la même Valeur que le Taux de l'Intérêt Conventionnel Annuel Fixé au Contrat et qu'avec eux il peut en Diverger !=> Dès lors à quoi sert un tel exemple capillotracté qui n'arrive jamais, mais alors jamais, dans la vie réelle, si ce n'est pour tergiverser, chercher "midi à quatorze heure" et "noyer le poisson".

Sur le ton de la plaisanterie, pour répondre à votre ironie, je vous retournerais la question :Friedrich a dit:Cher Monsieur,
j'aurais une toute petite question à vous poser.
Quand un quidam vous demande l'heure, à quel niveau de précision la lui indiquez-vous ? Heures + Minutes arrondies à un multiple de 5, à la minute près, minute + secondes (arrondies ou non), minutes, secondes, centièmes de secondes exactes ou arrondies, minutes + secondes + cent millème de seconde s, arrondies ou pas ... ?
A quel moment estimez - vous la précision nécessaire pour l'information apportée ?
Je reconnais que c'est un peu dommage, mais il me fallait étayer ma démonstration que vous pourrez relire à l'éclairage de ce que je vais vous écrire maintenant ! : Vous pourrez toujours la commenter après un regard nouveau ! :Voilà un peu ce que m'inspirent tous les travaux que vous publiez à longueur de page et auxquels je finis par ne plus comprendre un traitre mot du message que vous voulez faire passer ?
Bonne soirée.
Je vois que nos avis se rejoignent, ici ! ...Friedrich a dit:A titre tout à fait personnel, quand je paye mon pain, fait le plein de benzine, m'acquitte de mes agios ou encaisse mes salaires et dividendes, la précision au centime me suffit amplement.
Ai-je écrit cela ? : J'ai juste démontré, par tous ces Calculs successifs, que l'Hypothèse d'Aristide qui dit qu'il ne faut pas Arrondir tous les Montants Monétaires, affirmation péremptoire, ne tient pas la route, que c'est une Erreur de principe ! : Vous avez peut-être d'ailleurs remarqué qu'il a tenté vainement quelquefois de souligner des Erreurs de ma part dans cette démonstration, alors que c'est lui qui se fourvoyait totalement !Mais si vous dites qu'il y a un complot bancaire international, je veux bien vous croire.
L'ironie ne vous quitte donc jamais ?Combien vous dois-je, docteur ?
OK ! Alors, allons-y !Aristide a dit:Il faudrait être logique et cohérent dans tout le processus de calcul.

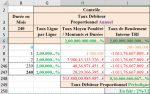



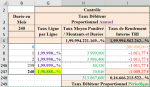


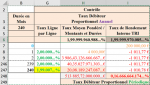
Avec toutes mes excuses, je viens, ici, rectifier, en Colonne H, le Tableau ci-dessus :Marioux a dit:1.2) Montant des Intérêts Périodiques Constant :
Afficher la pièce jointe 5587








 Enfin une bonne nouvelle pour le taux du Livret A, du LEP et du LDDS au 1er août 2026 ?
Enfin une bonne nouvelle pour le taux du Livret A, du LEP et du LDDS au 1er août 2026 ?
 Arnaque sur votre compte bancaire : la Cour de cassation tranche sur la responsabilité des banques
Arnaque sur votre compte bancaire : la Cour de cassation tranche sur la responsabilité des banques
 Retraite : « Les personnes non mariées n'ont pas le droit à la pension de réversion ? »
Retraite : « Les personnes non mariées n'ont pas le droit à la pension de réversion ? »
 « Virement de 357 » ou « 1 042 euros » : quand et de combien les aides de la CAF vont-elles augmenter ?
« Virement de 357 » ou « 1 042 euros » : quand et de combien les aides de la CAF vont-elles augmenter ?
 Le Livret A et le LEP vont financer le nucléaire, quel impact sur le rendement de votre épargne sans risque ?
Le Livret A et le LEP vont financer le nucléaire, quel impact sur le rendement de votre épargne sans risque ?
 Paiement mobile sans contact : Wero va concurrencer Apple Pay et Google Pay dès l'automne 2026
Paiement mobile sans contact : Wero va concurrencer Apple Pay et Google Pay dès l'automne 2026


