Bonsoir,
On va considérer que:
- Les dividendes sont payés le 31/12 ;
- Les dividendes ne sont pas retirés de l'enveloppe mais conservés sans rémunération.
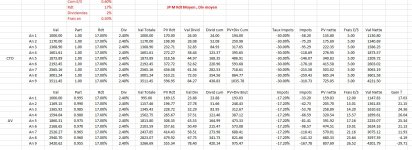
Une modélisation du CTO peut être la suivante: CTO{n} := R{n}*(1 - frais_transaction) - I{n} + D{n}, avec
- R{n} := K*(1 + r)^n * (1 - frais_transaction)
- I{n} := (R{n}- R(n-1)) * taux_flat_tax
- soit K*(1 + r)^(n-1) * (1 - frais_transaction) * r * taux_flat_tax
- D{n} := sum(R{n}* taux_dividende * (1 - taux_flat_tax), 1, n)
- soit somme d'une suite géométrique, donc K*(1-frais_transaction)*taux_dividende*(1- taux_flat_tax)* (1 - (1 + r)^n) / (1 - (1+r))
Avec r = 30%, taux_flat_tax = 30%, taux_dividende = 2%, frais_transaction = 0.08% (type Saxobank)
On obtient donc: CTO{n} := K*1.3^n*(1-0.0008)^2 - K*1.3^(n-1)*(1-0.0008)*0.3*0.3 + K*(1-0.0008)*0.02*0.7*(1 - 1.3^n) / (1-1.3)
Avec K = 1000, et n = 8, on obtient la somme nette d'imposition:
7913.71 EUR sur
CTO.
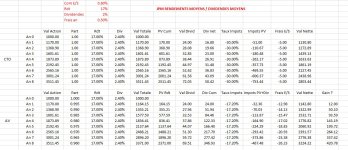
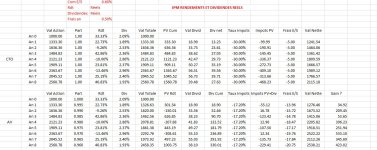
Une modélisation de l'AV peut être la suivante:
- R{n} := K*(1 - frais_transaction) * (1 + r*(1 - frais_gestion))^n
- D{n} := sum(R{n}* taux_dividende, 1, n)
- soit K*(1 - frais_transaction) * taux_dividende * (1 - (1 + r*(1 - frais_gestion))^n) / (1 - (1 + r*(1 - frais_gestion)))
- I{n} := max(R{n}*(1 - frais_transaction) - K*(1 - frais_transaction) + D{n} - abattement, 0) * (PFL + PS)
Avec r = 30%, taux_dividende = 2%, frais_transaction = 0.60%, frais_gestion=0.50%, PFL = 7.5%, PS = 17.2%, abattement = 4600 (seul)
On obtient donc: AV{n} := K*(1+0.3*(1-0.005))^n * (1-0.006)^2 - max(K*(1+0.3*(1-0.006))^n*(1-0.006)^2 - K*(1-0.006) + K*(1-0.006)*0.02*(1-(1+0.3*(1-0.005))^n)/(1-(1+0.3*(1-0.005))) - 4600, 0)*(0.075+0.172) + K*(1-0.006)*0.02*(1-(1+0.3*(1-0.005))^n)/(1-(1+0.3*(1-0.005)))
Avec K = 1000, et n = 8, on obtient la somme nette d'imposition:
7621.17 EUR sur
AV (type Linxea Spirit).
Avantage donc CTO. L'AV devient encore moins intéressante si K>150K EUR.
Seul intérêt de l'AV = succession.