Le Montant des Intérêts Périodiques doit-il être Arrondi où non ?

[Marioux]

Bonjour à tous,
Un Mois Civil déjà, 31 Jours Calendaires, et aucun retour ! Aucun avis, même contraire au mien, dans la discussion Taux d'Intérêt Conventionnel & Montants d'Intérêts Arrondis ? : Impossible ! ; Ce n’est pas Français ! ...
Il me faut bien l’avouer : Je reste perplexe quand je vois toute l’énergie développée pour trouver des Arguments Littéraires de la part des Emprunteurs ou des Avocats Défenseurs à l’encontre ou en faveur des Prêteurs, alors que si peu s’intéressent au Calcul Exact des Intérêts Périodiques dans un Échéancier, en particulier à leurs Arrondis, en tant que Valeurs Monétaires, qui en favoriserait la Compréhension et la Vérification ! :
Mais je ne désespère pas ! Et puis, après tout : "Qui ne dit mot consent" ! !...

Analysons l’incidence des Arrondis d’une Partie Seulement (Le Seul Montant des Échéances, cher à Aristide !) puis de Tous les Montants Monétaires d’un Échéancier ; Comme d’habitude on tentera de Simplifier au maximum en choisissant des Données Appropriées conduisant à des Résultats les plus parlants possibles pour tout un chacun :
Méthode dite du Mois Normalisé (Durée Fictive Mensuelle : 30 + 5/12 Jours) ; Calculs à 15 Chiffres Significatifs ;
Périodicité de Remboursement : Mensuelle ; Durée du Prêt : 3 Mois (Pour limiter la longueur de l’Échéancier ! ...) :
Prêt à Taux d’Intérêt Conventionnel Proportionnel Fixe Annuel : 3,65% (Soit 3,65%/A / 365J/A = 1%%/J ! ... ;
Capital Initial Emprunté : 10 000€ (Un Nombre Rond : 100 x 100€ ! ; 10 000€ x 1%%/J = 1€/J Exactement ! ...) ;
Date de Première Échéance : 25/03/2019 ; Date d’Échéance 0 Théorique : 25/02/2019 (1 Mois pile auparavant !) ;
Date de Réalisation : 25/02/2019 ; Nombre de Jours Intercalaires (Rompus ! ...) : (25/02/2019 - 25/02/2019) = 0 ;
Ces Dates ont été choisies de manière à faire apparaître les 3 Durées Civiles Mensuelles Différentes, 28, 30 et 31 Jours, existant Réellement dans une Année Commune de 365 Jours (Donc sans 29 Février, Jour Bissextil, l’oublié !)
Aucune Charge en dehors des Intérêts Conventionnels Simples (Ni Frais de Dossier, ni Assurance, ni Rien d’autre !)

6) Montants Monétaires Non Arrondis :
Aucun des Montants Monétaires n’est Arrondi (Sinon par la Précision de l’Outil de Calcul, l’Ordinateur !)
6.1) Paiement Périodique des Intérêts et de l’Amortissement du Principal :
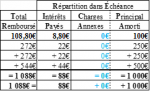
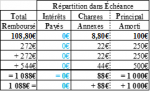
Le Tableau d’Amortissement qui en découle est le suivant :

_______________________
Montant des Échéances, Non Arrondi : 3 353,63 163 928 895…€/É (À 15 Chiffres Significatifs !) ;
Montant Global Théoriquement Acquitté : 3 353,63 163 928 895…€/É x 3É = 10 060,89 491 786 685…€ ;
Montant Total des Intérêts Théoriques : 10 060,89 491 786 685…€ - 10 000 € = 60,89 491 786 685…€ ;
Ajustement sur la Dernière Échéance ! : (10,16 970…€ + 3 343,46 194…€) - 3 353,63 164…€ = 0,00€ !

6.2) Cas d’un Prêt In Fine où Seuls les Intérêts sont Payés Périodiquement :
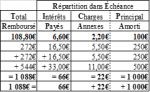
L’Échéancier qui en découle est le suivant :

_______________________
Montant Périodique des Intérêts Théoriques, Non Arrondi : 30,41 6…€/É ;
Montant Total des Intérêts Théoriques : 30,41 6…€/É x 3É = 91,25€ ;
Montant Global Théoriquement Acquitté : 10 000 € + 91,25€ = 10 091,25€ ;
Ajustement sur la Dernière Échéance ! : (30,41 666…€ + 10 000€) - 10 030,41 666…€ = 0,00€ !

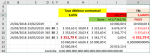
Dans ces Cas 6.1) et 6.2) le TEG (Taux Effectif Global Proportionnel Annuel) est Égal à 3,65% :
C’est Strictement la Valeur du TIC (Taux d’Intérêt Conventionnel Proportionnel Annuel Fixé au Contrat) !
Sans autre Charge que les Intérêts Conventionnels, le TEG est aussi Égal au Taux Débiteur Proportionnel Annuel !

Et là, attention, car Aristide intervient dans son Blog
Quelle est la bonne méthode pour vérifier que le taux nominal proportionnel contractuel d’un prêt est bien respecté ? :
"Dans la Pratique il va de soi que – au moins sur l’Échéance qui correspond à un flux réel de sortie de trésorerie – un Arrondi Monétaire à Deux Décimales sera toujours Indispensable."
Remarque "Judicieuse" ! : Entendons-la et retrouvons-nous, à ce sujet, au prochain épisode !
Cdt.

 

[paal]

Elles servent à quoi, toutes ces majuscules ??

 

[Marioux]

Bonjour paal,

Elles servent à quoi, toutes ces majuscules ??

Est-ce une critique ou une demande d’explication ? Faut-il vraiment que je vous réponde ? Oui ? Bien ! :
Pour le lecteur, toutes ces majuscules ne servent à rien ou, sans doute, pas à grand-chose, en fait ! : Je le reconnais.
J’espère simplement quelles ne sont pas perturbatrices au point de lui faire perdre le fil de la démonstration.

En tant que rédacteur, disons que, pour des raisons bien personnelles, on peut dire, si l’on veut, que c’est ma marque de fabrique, devenue un signe distinctif !
Mais surtout le temps passé à l’application de cette mise en forme me permet, simultanément, de réfléchir et limiter la quantité d’erreurs, déjà trop nombreuses, que je peux commettre et l’aspect visuel de la rédaction me facilite sa vérification à la relecture !
Comme vous voyez, cela part d’un bon sentiment mêlé certainement à un peu de perfectionnisme avec tout ce qu’il peut avoir de désagréable, quoi !

À chacun sa déformation, professionnelle ou non, son expression d’opinion et son choix de mise en forme ! Non ?
Pour d’autres ce sont, par exemple, la majoration de la police de caractères, qui fait penser qu’ils nous crient après, ou bien la multiplication répétée, tout aussi inutile, des signes de ponctuation (Mais en feriez-vous partie, ou avez-vous commis une faute de frappe ? ...) qui insinuent que l’on ne comprend pas suffisamment vite ou bien, l’emploi d’adjectifs qualificatifs désobligeants, voire le mépris par l’oubli de votre existence lorsqu’ils se sentent acculés dans leurs contradictions et retranchements !

Voilà, je crois avoir répondu de manière claire et franche à votre question.

Maintenant, je vous propose de passer à la suite de la démonstration, que j’ai essayé de rendre accessible, et dont je vous suggère de prendre connaissance afin de pouvoir me faire part de toute critique aussi sur le fond, comme des erreurs de raisonnement ou de calcul : Tout comme d’autres, je n’en suis pas à l’abri même si comme eux, à coup sûr, je fais de mon mieux !
Votre opinion peut être utile à tous : Elle sera donc la bienvenue, comme celle de tout lecteur intéressé !
Et les approbations éventuelles tout autant !
Cdt.

 

[Marioux]

Bonjour à tous,
Comme annoncé hier, reprenons les Cas 6) en arrondissant les Seuls Montants des Échéances et voyons l’incidence :
7) Montants Monétaires des Échéances Seuls Arrondis à 2 Décimales :
7.1) Paiement Périodique des Intérêts et de l’Amortissement du Principal :
__________________
Montant des Échéances, Arrondi à l’€C : 3 353,63€/É ; Montant Global Acquitté : 3 353,63€/É x 3É = 10 060,89€ ;
Montant Total des Intérêts Réellement Payés (Ici, Égal au Coût du Prêt !) : 10 060,89€ - 10 000€ = 60,89€ ;
Différence entre la Somme des Intérêts Périodiques Théoriques et ce Montant Total des Intérêts Réellement Payé :
60,89 493…€ - 60,89€ = 0,00 493…€ : Cette Divergence figure, ici, comme un Ajustement sur la Dernière Échéance !
7.2) Cas d’un Prêt In Fine où Seuls les Intérêts sont Payés Périodiquement :
__________________
Montant Périodique des Intérêts Réellement Payés, Arrondi à l’€C : ARRONDI (30,41 6…€/É ; 2) = 30,42€/É ;
Montant Total des Intérêts Réellement Payés (Ici, Égal au Coût du Prêt !) : 30,42€/É x 3É = 91,26€ ;
Montant Global Réellement Acquitté : 10 000€ + 91,26€ = 10 091,26€.
Différence entre la Somme des Intérêts Périodiques Théoriques et le Montant Total des Intérêts Réellement Payé :
91,26€ - 91,25€ = 0,01€ : Cette Divergence apparaît entre l’entre l’Échéancier et le Tableau des Taux Effectifs !
Aristide insiste, à la suite de son étude approfondie, en affirmant fermement :
"2) – L’arrondi monétaire à deux décimales au plus proche sur tous les éléments constitutifs du tableau d’amortissement
peut conduire à un taux réellement appliqué supérieur au taux nominal proportionnel contractuel ; Il est également à abandonner.
3) – La méthode d’arrondis la plus pertinente est l’arrondi monétaire à deux décimales au plus proche sur les échéances uniquement."
La Différence est Minime, certes, mais comment peut-on affirmer qu'Arrondir les Seuls Montants des Échéances permet de ne pas dépasser le Taux Débiteur Nominal alors que cela conduit, ici, à un Surcoût évident : Il faudra m'expliquer !

Par ailleurs, à la Vue et à la Lecture des Tableaux d’Amortissement des Cas 6.1) et 7.1), supposés fournis par un Prêteur, il est Impossible de Vérifier par un Calcul Inversé, Ligne par Ligne, le Taux d’Intérêt Exact (Avec Toutes ses Décimales !) pris en compte pour déterminer les Montants des Intérêts Périodiques, car Toutes les Décimales de ces derniers ne sont pas Affichées : Elles sont donc, a priori, Inconnues ! …

Dire que les Intérêts Périodiques ne sont pas à Arrondir, mais en faire Payer le Montant Arrondi à chaque Échéance, c’est quand même un peu fort de café ! Non ? : C’est, au mieux de la prestidigitation, au pire de l’embrouille. Là, Marioux s’en mêle :
"Les Montants Périodiques des Intérêts, implicitement et effectivement Arrondis (Ici, au Centime d’€uro !) dans les Échéances où ils sont les Seuls Payés (Différé d’Amortissement du Principal !), doivent l’être partout, sinon leur Somme diverge du Montant Global des Intérêts Réellement Payés !"
Remarque "Farfelue" ? : Examinons-la et, donc pour cela, à demain si vous le voulez-bien ! ...
Cdt.

 

[Marioux]

Bonjour à tous,
Comme promis, me voici pour Arrondir, cette fois, Tous les Montants Monétaires et en faire constater l’incidence :
8) Tous Montants Monétaires Arrondis à 2 Décimales :
Arrondir Tous les Montants Monétaires présente l’Intérêt de permettre la Vérification Directe, Certaine, Exacte et Indépendante, de Chaque Ligne du Tableau d’Amortissement, car Aucune Décimale n’y est Cachée ! ...
8.1) Paiement Périodique des Intérêts et de l’Amortissement du Principal :

Montant des Échéances Courantes, Arrondi à l’€C : 3 353,63€/ÉC, comme au cas 7.1) ! ;
Ajustement sur la Dernière Échéance (Seule impactée) : 0,01€ : La belle affaire, l’impact est on ne peut plus faible ! ;
La Valeur de cet Ajustement est d’ailleurs du même ordre de grandeur que la Différence constatée en 7.2) : Elles sont même Égales ! ...
Montant de la Dernière Échéance : 3 353,63€ + 0,01€ = 3 353,64€ ;
Montant Global Acquitté : 3 353,63€/ÉC x 2ÉC + 3 353,64€/DÉ = 3 353,63€/ÉC x 3ÉC + 0,01€ = 10 060,90€ ;
Montant Total des Intérêts Réellement Payé : 10 060,90€ - 10 000€ = 60,90€ ;
Et là, on retrouve une Stricte Égalité entre ce Montant Réellement Payé et la Somme des Intérêts Périodiques ! ...

Vérification manuelle Ligne à Ligne :
Échéance 1 :
Intérêts 1 : ARRONDI (10 000€ x 3,65%/A / 12M/A ; 2) = 30,42€ ;
Principal Amorti 1 : 3 353,63€ - 30,42€ = 3 323,21€ ;
Capital Restant Dû 1 : 10 000€ - 3 323,21€ = 6 676,79€ ;
Échéance 2 :
Intérêts 2 : ARRONDI (6 676,79€ x 3,65%/A / 12M/A ; 2) = 20,31€ ;
Principal Amorti 2 : 3 353,63€ - 20,31€ = 3 333,32€ ;
Capital Restant Dû 2 : 6 676,79€ - 3 333,32 = 3 343,47€ ;
Échéance 3 :
Intérêts 3 : ARRONDI (3 343,47€ x 3,65%/A / 12M/A ; 2) = 10,17€ ;
Principal Amorti 3 : 3 353,64€ - 10,17€ = 3 343,47€ ;
Capital Restant Dû 3 : 3 343,47€ - 3 343,47€ = 0€ : OK ! Le Taux d’Intérêt Conventionnel Annuel est bien Respecté !
8.2) Cas d’un Prêt In Fine où Seuls les Intérêts sont Payés Périodiquement :

On obtient Strictement les mêmes Valeurs suivantes qu’au cas 7.2) :
Montant Périodique des Intérêts Réellement Payés, Arrondi à l’€C : ARRONDI (10 000€ x 3,65%/A / 12M/A ; 2) = 30,42€/É ;
Montant Total des Intérêts Réellement Payé : 30,42€/É x 3É = 91,26€ ;
On retrouve encore une Stricte Égalité entre ce Montant Réellement Payé et la Somme des Intérêts Périodiques ! ...
Montant Global Acquitté : 10 000 € + 91,26€ = 10 091,26€ ;
Le Montant des Intérêts Mensuels étant Constant, la Vérification manuelle Ligne à Ligne est, ici, bien plus simple !

Taux Effectif Globalisé (Sur 3 Mois, la Durée Réelle du Prêt) : 91,26€ / 10 000 € = 0,009 126 = 0,91 26% ;
Taux Effectif Global (Annualisé, donc sur 12 Mois) : 0,91 26% x (12M / 3M) = 0,91 26% x 4 = 3,65 04% !

TEG : Égal à 3,64 971…% dans le Cas 7.1), 3,65 030…% dans le Cas 8.1) et 3,65 04% dans les Cas 7.2) et 8.2) ! :
Du fait de l’Arrondi des Montants Monétaires, dans tous ces Cas dans le même ordre de grandeur que le Taux d’Intérêt Conventionnel Proportionnel Fixe Annuel de 3,65%, le Taux Débiteur Proportionnel (Égal au TEG lorsqu’il n’y a pas de Charge Annexe !) en diverge donc très légèrement !

Cdt.

 

[Marioux]

Bonjour à tous,
Après un Intermède Arithmétique sur une autre discussion (Jurisprudence Année Lombarde [lien réservé abonné]) et un échange virulent dans la semaine, comme je le sous-entendais Dimanche dernier, il me semble nécessaire d’aborder dès maintenant la Méthode Exacte en l’appliquant, sur tout l’Échéancier, à chacun des Prêts Contractés avec les mêmes Hypothèses et dans les mêmes Conditions que ceux déjà traités jusqu’à présent par la Méthode dite du Mois Normalisé, afin d’en analyser l’incidence sur les Montants des Intérêts et les Taux Divers. Pourquoi pas ? Cela pourrait être instructif ! : C’est donc bien là que nous irons mais par un chemin détourné lié à l’intermède pour commencer ! ... :
L’annexe au décret N°2002-927 du 10 juin 2002 (JO du 11 juin 2002 - page 10358) et son Quatrième Exemple ! :
La Somme Prêtée le 1er Janvier 2001 (Année Commune de 365 Jours comme 2002 !) est de 1 000€ ;
Le Remboursement s’effectue en 3 Fois et les Montants à Payer par l'Emprunteur sont :
Après 3 Mois (1/4 d’Année/ 91,25 Jours !) : 272€, le 1er Avril 2001 ;
Après 6 Mois (1/2 d’Année/182,5 Jours !) : 272€, le 1er Juillet 2001 ;
Après 12 Mois (1 Année/365 Jours) : 544€, le 1er Janvier 2002.
Soit au Total de 1 088€ au bout d’un An.
L'équation est la suivante, avec des Fractions d’Exposants, exprimées Jours :

L'équation permet de calculer i par des approximations successives, qui peuvent être programmées sur une calculatrice de poche. On obtient : TAEG = 13,185 495…% (Affiché à 6 Décimales), et Arrondi :
TAEG = 13,185%, 13,19% ou 13,2%, selon la préférence sur la Précision et le Nombre de Décimales ! :
Dans, mon Calcul précédent, des Intérêts sur les 3 Échéances Apériodiques, détaillé au Post #2.118 [lien réservé abonné], a été effectué comme on peut le voir, par la Méthode dite du Mois Normalisé, tout comme le TAEG (Ici, Taux Débiteur Actuariel)
Aristide affirme "Dans votre calcul c'est 12,65% ; point barre !" :
C’est une Valeur, à 2 Décimales, effectivement bien plus probable pour un Taux d’Intérêt Conventionnel Annuel, Fixé a priori, que celle que j’ai employée, 12,649%, et que j’aurais pu, voire dû, Arrondir, de moi-même, à 12,65% ! : Soit ! ; Je reprends donc mes Calculs :
Première Échéance à 3 Mois :
Intérêts Période 1 = 1 000€ x 12,65% x 3M/12M = 31,62 5€ ~ 31,62€ ;
On remarquera, ici, l’Arrondi Inférieur, sinon on aboutit, au bout du Calcul, à 88,01€… !)
Et puis, si par un Calcul Inverse, Ligne à Ligne, on Vérifie le Taux d’Intérêt pratiqué dans cette Échéance après avoir Arrondi au Plus Proche, c’est-à-dire à 31,63€, on aurait : 31,63€ x 12M/3M / 1 000€ = 12,652% > 12,65% !
Il semble sage pour éviter toute contestation que le Prêteur Arrondisse les Intérêts Systématiquement à l’Inférieur !
Principal Amorti 1 : 272€ - 31 ,62€ = 240,38€ ;
Capital Restant Dû 1 : 1 000 € - 240,38€ = 759,62€.

Deuxième Échéance à 6 Mois :
Intérêts Période 2 = 759,62€ x 12,65% x 3M/12M = 24,02 298 25€ ~ 24,02€ ;
Principal Amorti 2 : 272€ - 24,02 = 247,98€ ;
Capital Restant Dû 2 : 759,62€ - 247,98€ = 511,64€.

Dernière Échéance à 12 Mois :
Intérêts Période 3 = 511,64€ x 12,65% x 6M/12M = 32,36 123€ ~ 32,36€ ;
Principal Amorti 3 : 1 000€ - 240,38€ - 247,98€ = 544€ - 32,36€ = 511,64€ ;
Capital Restant Dû 3 : 511,64€ - 511,64€ = 0€ : OK !

Montant Global des Échéances Réellement Payé : 272€ + 272€ + 544€ = 1 088€ ;
Montant Global des Intérêts Réellement Payé : 1 088€ - 1 000€ = 88€ !
Tout va bien, nous sommes en phase, à l’exception près de l’utilisation de l’Arrondi ! : Mais, où est le problème ?
Et par l’intermédiaire de la Fonction TRI d'Excel, bien utilisée, Sans autre Charge que les Intérêts Simples :
Taux Débiteur Actuariel Annuel : 13,185 495...%, Conforme au Résultat du quatrième exemple !
Taux Débiteur Proportionnel Annuel : 12,449 924...%, Différent de 12,65% ! :

Maintenant, dans la mesure où, dans ce Quatrième exemple, les Dates de Réalisation du Prêt et de Remboursements ainsi que le Montant de chacune des Échéances sont connus, le TAEG est invariable :
Comme on a supposé qu’il n’y pas de Charges Annexes, il est Égal au Taux Débiteur Actuariel Annuel !

Mais les Intérêts par Période peuvent très bien, comme Aristide le rappelle, être Calculés Réglementairement et Exactement (Aux Arrondis près !) par la Méthode Exacte dans la mesure où la Date de Départ est connue, le 01/01/2001, Date qu’il convient bien sûr de respecter, c’est la moindre des choses !
Et dans ce cas, si l’on reste sur ce Taux d’Intérêt Conventionnel Proportionnel Annuel de 12,65%, il est évident que, comme les Durées des Périodes dépendent de celles Variables des Mois Civils et non de celle Fictivement Constante des Mois Normalisés, les Intérêts par Période Varient par rapport à ceux de la Méthode dite du Mois Normalisé ! :
Première Échéance à 3 Mois (Du 01/01/2001 au 01/04/2001) :
Intérêts Période = 1 000€ x 12,65% x 90J / 365J/A = 31,19 178…€ ~ 31,19€ ;
Principal Amorti 1 : 272€ - 31,19€ = 240,81€ ;
Capital Restant Dû 1 : 1 000 € - 240,81€ = 759,19€.

Deuxième Échéance à 6 Mois (Du 01/04/2001 au 01/07/2001) :
Intérêts 2 = 759,19€ x 12,65% x 91J / 365J/A = 23,94 360 46…€ ~ 23,94€ ;
Principal Amorti 3 : 272€ - 23,94€ = 248,06€ ;
Capital Restant Dû 2 : 759,19€ - 248,06€ = 511,13€.

Dernière Échéance à 12 Mois (Du 01/07/2001 au 01/01/2002) :
Intérêts Période 3 = 511,13€ x 12,65% x 184J / 365J/A = 32,59 469…€ ~ 32,59€ ;
Principal Amorti 3 : 1 000€ - 240,81€ - 248,06€ = 511,13€ ;
Montant de l’Échéance : 32,59€ + 511,13€ = 543,72€ ;
Différence par rapport à la Méthode dite du Mois Normalisé : 543,72€ - 544€ = -0,28€ !
Capital Restant Dû 3 : 511,03€ - 511,03€ = 0€ : OK !

Montant Global des Échéances Réellement Payé : 272€ + 272€ + 543,72€ = 1 087,72€ ;
Montant Global des Intérêts Réellement Payé : 1 088€ - 1 000€ = 87,72€ #< 88€ !
Et là, il y a un Problème puisque le Montant Global des Intérêts Réellement Payé est en fait de 88€ #> 87,72€ :
Cela signifie que le Taux d’Intérêt Conventionnel Fixé et Réellement Appliqué est Supérieur à 12,65% !

Le Tableau des Taux Effectifs est très semblable au précédent : Il en Varie à la marge à partir de la 8ème Décimale du TAEG ! :
Quel est donc le Taux Réellement Appliqué ? À suivre …

 

[Marioux]

... Suite
L’Ordinateur et son Logiciel Excel répondent à la question et nous le disent : 12,689% #> 12,65% !

Première Échéance à 3 Mois (Du 01/01/2001 au 01/04/2001) :
Intérêts Période = 1 000€ x 12,689% x 90J / 365J/A = 31,28 794…€ ~ 31,28€ ;
Principal Amorti 1 : 272€ - 31,28€ = 240,72€ ;
Capital Restant Dû 1 : 1 000 € - 240,72€ = 759,28€.

Deuxième Échéance à 6 Mois (Du 01/04/2001 au 01/07/2001) :
Intérêts 2 = 759,28€ x 12,689% x 91J / 365J/A = 24,02 027…€ ~ 24,02€ ;
Principal Amorti 2 : 272€ - 24,02€ = 247,98€ ;
Capital Restant Dû 2 : 759,28€ - 247,98€ = 511,30€.

Dernière Échéance à 12 Mois (Du 01/07/2001 au 01/01/2002) :
Intérêts Période 3 = 511,30€ x 12,689% x 184J / 365J/A = 32,70 605…€ ~ 32,70€ ;
Principal Amorti 3 : 1 000€ - 240,72€ - 247,98 = 511,30€ ;
Montant de l’Échéance : 32,70€ + 511,30€ = 544€ ;
Capital Restant Dû 3 : 511,30€ - 511,30€ = 0€ : OK !

Montant Global des Échéances Réellement Payé : 272€ + 272€ + 544€ = 1 088€ ;
Montant Global des Intérêts Réellement Payé : 1 088€ - 1 000€ = 88€ !
Bien évidemment, l’Hypothèse a été prise qu’il n’y avait aucune Charge en dehors des Intérêts Simples !
Si tel n’était pas le Cas, la copie serait à revoir : Le TAEG ne serait pas Égal au Taux Débiteur Actuariel Annuel !

Remarque : Au passage, on remarque que l'Année 2000 est Bissextile, ce n'est pas pris en compte par le Législateur dans son exemple !
Cdt.

 

[Aristide]

???

 

[Aristide]

ERRATUM sur année civile

 

[Marioux]

Bonjour à tous,
"Mais pourquoi faites-vous donc cette Remarque en dernière minute sur l’Année 2000, non prise en compte par le Législateur alors que le Prêt concerné par son Quatrième exemple se déroule en 2001 ?", me direz-vous !
"Eh bien ! justement, parce que si cela avait été le cas qu’il se déroule en 2000, Année Bissextile, dans la mesure où il utilise la Méthode dite du Mois Normalisé, ses Calculs et Résultats seraient Strictement les mêmes malgré la Différence de Durée de ces Années Civiles : Or 366 # 365, que je sache ! ; Par cette Méthode, le 29 Février 2000, Jour Bissextil, passe délibérément à la trappe !"
Par la Méthode Exacte, il aurait bien fallu, en tenir compte et prendre le Diviseur 366 au lieu de 365, ce qui aurait modifié la Divergence par rapport à la Méthode dite du Mois Normalisé : Quel est donc le Taux Appliqué ? L’Ordinateur et son Logiciel Excel nous le disent : 12,672% #> 12,65% !

Première Échéance à 3 Mois (Du 01/01/2000 au 01/04/2000) :
Intérêts Période 1 = 1 000€ x 12,672% x 91J / 366J/AB = 31,50 688 524 590…€ ~ 31,50€ (Arrondi Inférieur !) ;
Principal Amorti 1 : 272€ - 31,50€ = 240,50€ ;
Capital Restant Dû 1 : 1 000€ - 240,50€ = 759,50€.

Deuxième Échéance à 6 Mois (Du 01/04/2000 au 01/07/2000) :
Intérêts Période 2 = 759,50€ x 12,672% x 91J / 366J/AB = 23,92 947 934…€ ~ 23,92€ (Arrondi Inférieur !) ;
Principal Amorti 2 : 272€ - 23,92€ = 248,08€ ;
Capital Restant Dû 2 : 759,50€ - 248,08€ = 511,42€.

Dernière Échéance à 12 Mois (Du 01/07/2000 au 01/01/2001) :
Intérêts Période 3 = 511,42€ x 12,672% x 184J / 366J/AB = 32,58 063 989 508…€ ~ 32,58€ ;
Principal Amorti 3 : 1 000€ - 240,50€ - 248,08€ = 511,42€ ;
Montant de l’Échéance : 32,58€ + 511,42€ = 544€ ;
Différence par rapport à la Méthode dite du Mois Normalisé : 544€ - 544€ = 0€ !
Capital Restant Dû 3 : 511,42€ - 511,42€ = 0€ : OK !

Montant Global des Échéances Réellement Payé : 272€ + 272€ + 544€ = 1 088€ ;
Montant Global des Intérêts Réellement Payé : 1 088€ - 1 000€ = 88€ !
Le Taux d’Intérêt Conventionnel Fixé et Réellement Appliqué (12,672%) est donc, ici aussi, Différent et Supérieur à 12,65% !

Mais cela peut aller beaucoup plus loin encore :
Comme je le disais hier, pour le Montant de chacune des 3 Échéances, dans l’énoncé de ce Quatrième exemple, rien n’est précisé concernant la Répartition (Intérêts Payés, Charges Annexes, Principal Amorti) : L’Hypothèse prise a été qu’il n’y avait aucune Charge en dehors des Intérêts Simples ! : Mais si tel n’était pas le Cas, la copie serait bien évidemment à revoir : Le TAEG, toujours de 13,185 495% ne serait plus Égal au Taux Débiteur Actuariel Annuel ! ; En fait, comme son nom l’indique, il est Effectif et Global et ne permet pas de faire la part des choses.
Les Parties sont libres d’avoir Négocié et Porté au Contrat les Conditions du Prêt, que nous n’avons pas lues !
L’Échéancier pourrait se décomposer, sans distinction de TAEG, selon l’un des 3 Tableaux suivants, par exemple :

Dans l’incertitude, comment peut-on penser déterminer le Taux d’Intérêt Débiteur Proportionnel ou Actuariel ?
Cdt.

 

[Aristide]

Et par l’intermédiaire de la Fonction TRI d'Excel, bien utilisée, Sans autre Charge que les Intérêts Simples :
Taux Débiteur Actuariel Annuel : 13,185 495...%, Conforme au Résultat du quatrième exemple !
Taux Débiteur Proportionnel Annuel : 12,449 924...%, Différent de 12,65% ! :

 

[Marioux]

Bonjour à tous,
L’étude précédente du Quatrième exemple du Législateur, bien qu’instructive, se situait finalement sur un chemin de traverse par rapport au chemin détourné qu’il était prévu d’emprunter : Revenons donc à ce dernier sur lequel nous pensions traiter le Remboursement d’un Prêt de 10000€ en 3 Échéances Mensuelles dont les Intérêts "Périodiques" seraient Calculés par la Méthode Exacte, ce qui est "parfaitement légal et juste" d’après Aristide ! ...
Repartons des Cas 6) en leur appliquant cette Méthode Exacte pour le Calcul des Intérêts Périodiques :
9) Montants Monétaires Non Arrondis ; Calcul des Intérêts Périodiques par la Méthode Exacte :
Aucun des Montants Monétaires n’est Arrondi (Sinon par la Précision de l’Outil de Calcul, l’Ordinateur !)
Le Montant des Intérêts Périodiques est Proportionnel à la Durée Réelle Mensuelle, en Nombre de Jours.
9.1) Paiement Périodique des Intérêts et de l’Amortissement du Principal :
Pour permettre une comparaison fiable avec le Cas 6.1), il convient de conserver le même Montant Théorique des Échéances Courantes (À 15 Chiffres Significatifs !), quitte à Ajuster, si nécessaire, le Montant de la Dernière.
Le Tableau d’Amortissement qui en découle est le suivant :

Montant Théorique des Échéances Courantes, Non Arrondi : 3 353,63 163 928 895…€/ÉC ;
Montants Périodiques des Intérêts Théoriques : 28,00 000…€, 20,69 054…€ et 10,02 428…€ ;
Montant Total des Intérêts Théoriques : 28,00 000…€ + 20,69 054…€ + 10,02 428…€ = 58,71 482…€ ;
Montant Global Théoriquement Acquitté : 10 000 € + 58,71 482…€ = 10 058,71 482…€ ;
Montant Théorique par Échéance de l’Amortissement du Principal, Non Arrondi :
Première Échéance : 3 353,63 163 928 895…€/ÉC - 28,00 000…€ = 3 325,63 164…€ ;
Deuxième Échéance : 3 353,63 163 928 895…€/ÉC - 20,69 054…€ = 3 332,94 110…€ ;
Dernière Échéance : 10 000 € - 3 325,63 164…€ - 3 332,94 110…€ = 3 341,42 726…€ ;
Montant Théorique Dernière Échéance : 10,02 428…€ + 3 341,42 726…€ = 3 351,45 155…€ ;
Ajustement Théorique sur la Dernière Échéance ! : 3 351,45 155…€ - 3 353,63 164…€ = -2,18 009…€ !
Le Coût du Prêt est Inférieur à celui du Cas 6.2) de cette Dernière Valeur, ce qui fait penser à un TEG moindre ! :
Ceci est confirmé par le Tableau des Taux Effectifs (Précis à 5 Décimales près seulement) :
TEG : 3,51 984 < 3,65% ! ; Différence : 3,65% - 3,51 984% = 0,13 016% > 0,1% !
Si le Prêteur choisit un Affichage à 2 Décimales, la Valeur Réelle Arrondie du TEG est de 3,52% et compte tenu de la Tolérance admise de 0,1%, la plage de Validité de son Affichage va de 3,42% à 3,62% !
On remarque que le Taux d’Intérêt Conventionnel Annuel, contracté à 3,65%, n’est pas dans cette plage ! :
Que faut-il en penser ? : La question est posée aux Spécialistes du Calcul Financier !
Quant à moi, sachant que, dans cet exemple simplifié, il n’y a Aucune Charge en dehors de celle des Intérêts Simples, donc que le Taux Effectif Global est Égal au Taux Débiteur Proportionnel, je persiste, signe et enfonce le clou ! :
Le Taux Débiteur est une Entité Différente de celle du Taux d’Intérêt Conventionnel !
Désolé pour eux, mais il va falloir qu’un (beau) jour, Membre39498 et, surtout, Aristide se remettent en question ! ...
9.2) Cas d’un Prêt In Fine où Seuls les Intérêts sont Payés Périodiquement :
L’Échéancier qui en découle est le suivant :

Montants Périodiques des Intérêts Théoriques, Non Arrondis (La Proportionnalité est assez apparente !) :
Échéance 1 : 10 000€ x 28J x 1%%/J = 28,00 000…€ ;
Échéance 2 : 10 000€ x 31J x 1%%/J = 31,00 000…€ ;
Échéance 3 : 10 000€ x 30J x 1%%/J = 30,00 000…€.
Montant Total des Intérêts Théoriques : 28,00 000…€ + 31,00 000…€ + 30,00 000…€ = 89,00 000…€ ;
Toutes les Décimales sont Nulles (0), c’est une évidence si l’on se penche un tant soit peu sur le détail des Calculs !
Dans ce Cas et à ce stade, nous pouvons remarquer, au passage, que si nous avions Arrondi les Seuls Montants des Intérêts Périodiques, au Centime d’€uro près, voire même à l’€uro près, cela n’aurait eu absolument Aucune Incidence sur le Tableau d’Amortissement, les Montants des Échéances et donc sur le Tableau des Taux Effectifs :

Montants Périodiques des Intérêts Payés (La Proportionnalité est, ici, on ne peut plus visible !) :
Échéance 1 : ARRONDI (10 000€ x 28J x 1%%/J ; 2) = 28€ ;
Échéance 2 : ARRONDI (10 000€ x 31J x 1%%/J ; 2) = 31€ ;
Échéance 3 : ARRONDI (10 000€ x 30J x 1%%/J ; 2) = 30€.
Montant Total des Intérêts Payés : 28€ + 31€ + 30€ = 89€ (Coût du Prêt pour une Durée Globale de 89J ! ...)
Ce Montant est à comparer avec celui obtenu dans le Cas 6.2) par la Méthode dite du Mois Normalisé : 91,25€ !
La Différence est de 91,25€ - 89€ = 2,25€ ! La Divergence est de 2,25€ / 89€ = 0,02 528% soit 2,528% !
Montant Global Acquitté : 10 000€ + 89€ = 10 089€.
Ajustement sur la Dernière Échéance ! : (30,00€ + 10 000€) – 10 030,00€ = 0,00€ !
TEG : 3,55 976 280…% < 3,65% ! ;
Différence : 3,65% - 3,55 976 280…% = 0,09 023 720…% < 0,1% (Mais très Proche et dans le bon sens ! ...)
Pour un même Taux d’Intérêt Conventionnel Proportionnel Fixe Annuel, selon la Méthode de Calcul des Intérêts Périodiques, le TEG Varie tout en restant Exact ! Sa plage de Variation peut dépasser 0,1%, sa Tolérance admise !
Sachant qu’ici, comme il n’y a pas de Charge Annexe, le TEG est Égal au Taux Débiteur Proportionnel Annuel, ce dernier Diverge du Taux d’Intérêt Conventionnel Proportionnel Annuel ! : Ce sont donc bien 2 Entités Différentes !
La prochaine fois, on parle Intérêts Intercalaires, promis, juré !
Cdt.

 

[Aristide]

Et par l’intermédiaire de la Fonction TRI d'Excel, bien utilisée, Sans autre Charge que les Intérêts Simples :
Taux Débiteur Actuariel Annuel : 13,185 495...%, Conforme au Résultat du quatrième exemple !
Taux Débiteur Proportionnel Annuel : 12,449 924...%, Différent de 12,65% !

 

[Aristide]

Quelle est la bonne méthode pour vérifier que le taux nominal proportionnel contractuel d’un prêt est bien respecté ?

1) – Dans l’absolu, pour le calcul du taux nominal proportionnel, le taux de rendement Interne (TRI) n’est pas le critère le plus fiable/pertinent ; il est donc à exclure.

Mais, quand il s’agit de comparer des offres concurrentes, en valeurs relatives donc, ce critère reste parfaitement acceptable.

Toutes choses étant égales par ailleurs, avec cette même méthode appliquée aux cas en présence, même si en valeur absolue le taux qui en résulte n’est pas parfaitement exact, l’orientation restera bonne ; le taux le plus faible restera le plus faible et la même chose pour le taux le plus fort.

[lien réservé abonné]

Pour résumer et conclure:

1) - Le taux débiteur = taux nominal proportionnel = taux contractuel c'est la même chose.

2) - Ce taux ne se calcule pas.

3) - Il se négocie et est formalisé dans un contrat

4) - De ce fait il doit être respecté et donc ne doit pas être dépassé; en revanche une banque a tout à fait la possibilité de procéder à un abandon partiel de quelques euros/fractions d'euros pour respecter cette contrainte.

5) - Dès lors la méthode d'arrondi doit être adaptée à cette fin.

6) - Pour vérifier si le taux débiteur respecte bien le contrat le Taux de Rendement Interne (TRI) n'est fiable que pour des échéances pleines et constantes et avec une périodicité régulière.

Dans tous les autres cas ce TRI n'est pas pertinent.

Il reste trois moyens de procéder à cette vérification:
+ Recalcul ligne par ligne
+ Calcul taux moyen pondéré - par les montants et durées - d'ensemble
+ Calcul itératif ainsi qu'expliqué ci-dessus.

https://www.moneyvox.fr/forums/fil/jurisprudence-annee-lombarde.35089/page-213#post-336601

 

[Anonyme]

:
Le Taux Débiteur est une Entité Différente de celle du Taux d’Intérêt Conventionnel !
Désolé pour eux, mais il va falloir qu’un (beau) jour, Membre39498 et, surtout, Aristide se remettent en question ! ...

Je n’ai pas le loisir de me pencher sur vos calculs, certainement très intéressants sur le plan théorique, mais qui ne sont pas exploitables dans un contentieux judiciaire. Je peux en revanche vous assurer, après de nombreuses années de pratique, que pour les juristes, taux conventionnel, taux nominal et taux débiteur sont synonymes ; voir entre des centaines d’exemples :

- un extrait d’un arrêt de la CA DOUAI 10 Octobre 2019 – n° 17/01543 : « l'écart entre les dates utilisées pour le calcul dudit taux, ainsi que pour celui du taux débiteur, autrement dit du taux conventionnel, est exprimé en années ou en fractions d'années »

- un extrait du Juris-Classeur Commercial Fasc. 356 : RÉMUNÉRATION DU PRÊTEUR par Dominique Legeais - Professeur à l'université Paris V, René Descartes n° 33 : « Le TEG se distingue ainsi du taux nominal ou taux conventionnel qui correspond au taux vu du côté du banquier ».

 

[Aristide]

Bonjour casaminor,

Non seulement je suis parfaitement d'accord avec vous mais j'ai démontré que le TRI ne permet pas de retrouver le taux débiteur = taux nominal proportionnel = taux conventionnel.

En premier, et vous le savez bien car nous avons déjà échangé sur le sujet, la fonction TRI de Excel ne permet un calcul exact du TRI que si les échéances sont avec une périodicité régulière.
.
Sur ce point, curieusement, l'on assiste à une belle tentative de pirouette mais qui ne marche pas !!!

Ensuite l'on voit bien dans l'exemple fourni que, par trois méthodes différentes, l'on retrouve bien le taux contractuel mais pas avec le TRI qui - sur 3 mois - est fortement impacté par la troisième échéance minorée.

Pour ce qui me concerne ce sera ma dernière intervention sur le sujet.

Cdt

 

[Marioux]

Bonjour Membre39498,

Je n’ai pas le loisir de me pencher sur vos calculs, certainement très intéressants sur le plan théorique, mais qui ne sont pas exploitables dans un contentieux judiciaire. Je peux en revanche vous assurer, après de nombreuses années de pratique, que pour les juristes, taux conventionnel, taux nominal et taux débiteur sont synonymes ; voir entre des centaines d’exemples :
- un extrait d’un arrêt de la CA DOUAI 10 Octobre 2019 – n° 17/01543 : « l'écart entre les dates utilisées pour le calcul dudit taux, ainsi que pour celui du taux débiteur, autrement dit du taux conventionnel, est exprimé en années ou en fractions d'années »
- un extrait du Juris-Classeur Commercial Fasc. 356 : RÉMUNÉRATION DU PRÊTEUR par Dominique Legeais - Professeur à l'université Paris V, René Descartes n° 33 : « Le TEG se distingue ainsi du taux nominal ou taux conventionnel qui correspond au taux vu du côté du banquier ».

Décidemment, il n’est pas facile de convaincre des Spécialistes !
Entre Aristide qui affirme, encore une fois péremptoirement, que la Fonction TRI d’Excel ne permet pas de retrouver le Taux d’Intérêt Conventionnel Proportionnel Annuel Fixé au Contrat et Vous qui m’avouez n’avoir pas le loisir de vous pencher sur mes Calculs, alors que vous débattez depuis si longtemps avec lui, sans vous accorder sur le Calcul des Intérêts Intercalaires, cela fait beaucoup !
Si mes Calculs étaient si Faux, comment peut-on expliquer que dans le Quatrième exemple du Législateur, précédemment étudié, lorsque je Calcule le TAEG par sa Formule, je trouve comme lui (13,18 549 545 275 93…%) et que par l’Intermédiaire de la Fonction TRI j’arrive au même Résultat (13,18 549 544 335 33…%) sachant que la Précision annoncée par Microsoft sur TRI est de 0,00 001% !

Est-il trop vous demander de bien vouloir vous pencher un minimum sur le seul Exemple suivant qui répond à la critique d’Aristide ?
Vous pourrez y constater que contrairement à ce qu’il affirme, par la Fonction TRI d’Excel, on retrouve bien, en Calculant le Taux Débiteur Proportionnel, la Valeur du Taux d’Intérêt Conventionnel Proportionnel Annuel Nominal Fixé au Contrat, si les Conditions Nécessaires sont réunies (Celles d’une Réelle Périodicité !) ! ...
Capital Initial Emprunté : 10 000€ ; Taux d’Intérêt Conventionnel Proportionnel Annuel Fixé à 3,65% ;
Remboursement en 3 Échéances Réellement Périodiques ; Périodicité : 30 Jours Calendaires (Civils)
Date de Réalisation : 23/02/2019 ; Date des Échéances : 25/03/2019 ; 24/04/2019 et 24/05/2019 !
Amortissement Réellement Périodique :

Amortissement In Fine ; Intérêts Réellement Périodiques :

Dans les 2 Cas :
Taux d’Intérêt Débiteur Périodique : 100 x 30€ / 10 000€ = 0,3% ;
Taux d’Intérêt Débiteur Annuel : 0,3% x 365 / 30 = 3,65% !
Ce dernier, Égal au Taux d’Intérêt Conventionnel Proportionnel Annuel, Fixé au Contrat !

Pourquoi en est-il ainsi ? : Tout simplement parce qu’il s’agit, ici, de Remboursements Réellement Périodiques, alors que les Remboursements Mensuels ne le sont pas (28 ou 29, 30 et 31 Jours ! ; Leurs flux de trésorerie n’interviennent pas à Intervalles Réguliers sauf à considérer des Mois Normalisés ! ; Ils ne sont dans ce cas que Fictivement Périodiques de Périodicité Fictive 30 5/12 Jours !)
À partir du moment où l’Instrument de Mesure du TEG et du Taux Débiteur Proportionnel est faussé, puisqu’il part sur la Base dite du Mois Normalisé quand les Remboursements sont Mensuels, forcément le Résultat de la Mesure est faussé lui aussi : On ne retombe pas sur ses pieds ! L’Erreur produite sur la Mesure est reconduite pour chacun des Prêts Comparés !

Vous pouvez aussi simuler le même Prêt Remboursé avec, par exemple, des Périodicités quelconques, par exemple 27, 28, 29, 30, 31, 32 ou 73 Jours, et vous retomberez systématiquement sur le Taux d’Intérêt Conventionnel Proportionnel Annuel Nominal, Fixé au Contrat !
Au TEG correspond le Taux Débiteur Proportionnel et au TAEG correspond le Taux Débiteur Actuariel !
Tous ces Taux sont Calculés sur la Base dite du Mois Normalisé et leurs Valeurs sont perturbées par l’Instrument de Mesure !
Les Arrondis et la Non-Périodicité du Mois Normalisé provoquent des Divergences de Taux qui s’expliquent Mathématiquement !
Cdt.

 

[Marioux]

Bonjour Membre39498,

Je n’ai pas le loisir de me pencher sur vos calculs, certainement très intéressants sur le plan théorique, mais qui ne sont pas exploitables dans un contentieux judiciaire. Je peux en revanche vous assurer, après de nombreuses années de pratique, que pour les juristes, taux conventionnel, taux nominal et taux débiteur sont synonymes ; voir entre des centaines d’exemples :
- un extrait d’un arrêt de la CA DOUAI 10 Octobre 2019 – n° 17/01543 : « l'écart entre les dates utilisées pour le calcul dudit taux, ainsi que pour celui du taux débiteur, autrement dit du taux conventionnel, est exprimé en années ou en fractions d'années »
- un extrait du Juris-Classeur Commercial Fasc. 356 : RÉMUNÉRATION DU PRÊTEUR par Dominique Legeais - Professeur à l'université Paris V, René Descartes n° 33 : « Le TEG se distingue ainsi du taux nominal ou taux conventionnel qui correspond au taux vu du côté du banquier ».

Bonjour Membre39498,
Je ne voudrais pas que vous puissiez penser que, moi aussi, je me défile en ne commentant pas les sources que vous avez fournies :

- un extrait d’un arrêt de la CA DOUAI 10 Octobre 2019 – n° 17/01543 : « l'écart entre les dates utilisées pour le calcul dudit taux, ainsi que pour celui du taux débiteur, autrement dit du taux conventionnel, est exprimé en années ou en fractions d'années »

Ce n’est pas ce qui est écrit dans les Textes Officiels :
"Décret n° 2016-607 du 13 mai 2016 portant sur les contrats de crédit immobilier aux consommateurs relatifs aux biens immobiliers à usage d'habitation [lien réservé abonné]
ANNEXE II
PARTIE III
Calcul du taux annuel effectif global (TAEG) pour les crédits encadrés par les articles L. 313-1 et suivants
c) L'écart entre les dates utilisées pour le Calcul du TAEG, ainsi que pour Celui du Taux Débiteur , est exprimé en années ou en fractions d'années"
Le Taux Débiteur n'est donc pas Fixé puisque Calculé !
Implicitement, ici, il est question du Taux Débiteur Actuariel, puisqu'il est Calculé, comme le TAEG, par Actualisation des Flux.
Il ne peut être le Taux d'Intérêt Conventionnel Proportionnel.
Il s’agit donc là d’une extrapolation mal venue !

- un extrait du Juris-Classeur Commercial Fasc. 356 : RÉMUNÉRATION DU PRÊTEUR par Dominique Legeais - Professeur à l'université Paris V, René Descartes n° 33 : « Le TEG se distingue ainsi du taux nominal ou taux conventionnel qui correspond au taux vu du côté du banquier ».

Ce n’est nullement écrit comme cela dans aucun Texte Officiel ! ; Il s’agit, là encore d’une Interprétation Erronée !
Tels qu’ils ont été conçus par le Législateur, le TEG et le TAEG ne se distinguent de leur Taux Débiteur Associés, Respectivement Proportionnel et Actuariel (Basés sur les Seuls Intérêts Simples), qu’en ce qu’ils prennent en compte, en sus, les Charges Annexes Obligatoires ou Imposées par le Prêteur (Frais de Dossier, Assurances Diverses, etc.) !
"Le Taux vu du côté du Banquier", c’est celui qui permet de Calculer Directement le Montant des Intérêts de chaque Échéance, qu’elle ait été prédéfinie ou non, c’est-à-dire le Taux de l’Intérêt Conventionnel introduit par l’article 1907 du Code Civil Créé par Loi 1804-03-09 promulguée le 19 mars 1804 (Ce n’est pas récent !)
"L'intérêt est légal ou conventionnel.
L'intérêt légal est fixé par la loi.
L'intérêt conventionnel peut excéder celui de la loi, toutes les fois que la loi ne le prohibe pas.
Le Taux de l'Intérêt Conventionnel doit être Fixé par écrit."
Alors que le Taux de l’Intérêt Conventionnel soit :
Nominal : Pourquoi pas ? : Cela n’en change pas les Propriétés ;
Annuel : Pourquoi pas, non plus ? : Pour comparer des Offres Concurrentes entre-elles il faut bien instituer une Base de Référence !
Encore faudrait-il s’entendre de façon définitive et uniforme sur le sens de ce mot Annuel !
Quand on voit la valse des Nombres pour le préciser, nous ne sommes pas au bout de nos peines :
360 ; 365 ; 366 ; sachant que les Mois en représentent 1/12ème, donc 30 ; 30 5/12 ; 30,5 ; quand ils n’en font pas 28, 29 ou 31 !
Je vous assure, il y a du ménage à faire !
Exprimer le Taux d’Intérêt Conventionnel sur la Base de 100 Jours Civils (Calendaires) auraient été 100 Fois mieux approprié pour une Entité exprimée en Pourcentage (Pour Cent Jours !) !
Et quand j’écris "100 Fois", ce n’est qu’une expression : Essayez d’imaginer alors les économies de Procédures car les Calculs seraient Indiscutables !
Proportionnel : Oui, bien sûr ! : Encore, là-aussi, faudrait-il qu’il le soit Réellement, aux Nombres de Jours (Pourquoi pas ?), ce qui n’est pas le Cas avec la Méthode dite du Mois Normalisé !
Débiteur : N’en parlons pas, car, enfin, pourquoi donc employer un Terme Différent de celui du Code Civil, compréhensible par le commun des mortels, si c’était la même Entité ? : Pour créer la confusion une fois de plus ?
De la part des Banquiers, il n’y aurait, là, rien d’étonnant ; Il leur faut bien garder la maîtrise de la Finance !...
Cdt.

 

[Aristide]

?

 

[Marioux]

Bonjour Aristide et bienvenu, je vous l’assure,

?

"Faux comme d’habitude" : Voulez-vous parler de la Cellule K6, où figure la Formule Erronée "=K12*12" que j’ai reportée dans la Cellule J6 en rouge, au lieu la Formule Appropriée "=K12*365/30" portée dans la Cellule J7 en vert ? :

Je vous l’ai déjà dit je ne suis pas à l’abri d’Erreurs, et je suis prêt à les reconnaître quand je me suis trompé, mais de là à endosser celles des autres, je suis moins d’accord !
Cdt.